| 6 |
The respiratory chain |
| 6.1 |
Introduction |
In the respiratory chain, the NADH and FADH2 that was accumulated in the preceding degradative pathways is finally disposed of by reacting it with molecular oxygen. The free energy of this “cold combustion” is used to generate ATP. The amount of ATP generated in the respiratory chain far exceeds the modest quantities produced in the upstream pathways; this is the reason why only aerobic metabolism enables us to sustain physical exertion for extended periods of time.
The workings of the respiratory chain are quite different from all other pathways in human metabolism. Each of those other pathways consists of a succession of discrete enzymatic reactions. Inasmuch as these pathways contribute to the production ATP, the energy is always passed from one energy-rich bond to the next, with a newly created phosphoanhydride bond in ATP as the final recipient. In contrast, the respiratory chain combines chemical reactions with physical forces that are not pinned down to individual molecules, and the energy is stored and converted in novel ways.
| 6.2 |
Overview |
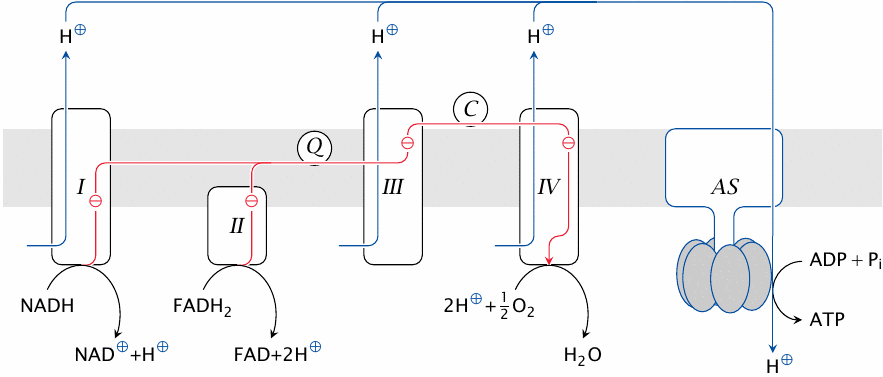
The respiratory chain involves four large protein complexes (I–IV) as well as ATP synthase (AS). All of these are embedded in the inner mitochondrial membrane. Coenzyme Q (Q) and cytochrome C (C) are diffusible electron carriers.
In this scheme, the mitochondrial matrix is below the membrane, whereas the cytosol is above it. The reactions carried out in the chain are explained below. Note that the reactants in this scheme are not stoichiometrically balanced.
| 6.2.1 |
Functional stages in the respiratory chain |
- H2 is abstracted from NADH+H+ and from FADH2
- The electrons obtained with the hydrogen are passed down a cascade of carrier molecules located in complexes I–IV, then transferred to O2
- Powered by electron transport, complexes I, III, and IV expel protons across the inner mitochondrial membrane
- The expelled protons reenter the mitochondrion through ATP synthase, driving ATP synthesis
The electron transport chain (ETC) comprises complexes I–IV. Hydrogen is acquired by complexes I and II from NADH and FADH2, respectively. The electrons are then passed down the chain to complex IV, which transfers them to molecular oxygen; the reduced oxygen then reacts with protons to yield water.
Complexes I, III and IV extract energy from the electron flow and use it to expel protons across the membrane. For each electron migrating down the chain, multiple protons are pumped out of the mitochondrion. The protons accumulated outside the mitochondrion are allowed back in through ATP synthase. This protein is a molecular motor, driven to rotate by the flow of protons through it into the mitochondrial matrix. The rotary motion of ATP synthase in turn drives the synthesis of ATP from ADP and phosphate.27
If you think that all this sounds somewhat strange and vague, you are quite right—but don’t let that trouble you. The purpose of this overview is only to divide and conquer, to break up the overall process into manageable parts that we can then tackle in detail in their turn.
| 6.3 |
ATP synthesis can be separated from electron transport |
The first thing to note about electron transport and ATP synthesis is that they can be experimentally separated from one another. So-called uncoupling agents allow the observation of electron transport without ATP synthesis. On the other hand, ATP synthesis works without electron transport if a proton gradient is created in some other way.
| 6.3.1 |
Uncoupling proteins dissipate the proton gradient |
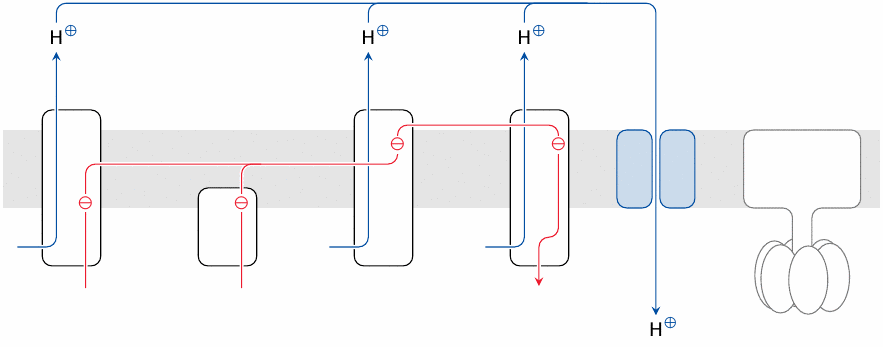
Uncoupling proteins are membrane proteins, also embedded in the inner mitochondrial membrane, that passively transport protons, allowing them to bypass ATP synthase. Electron transport and hydrogen oxidation—and, upstream of it, degradation of energy-rich substrates—will continue, but ATP synthesis will cease; the energy that would have gone into ATP synthesis is simply dissipated as heat.
Uncoupling proteins are found in particularly high concentration in the mitochondria of brown fat tissue, which differs from the more abundant white fat tissue by its high density of mitochondria.28 Brown fat tissue serves the purpose of producing heat, by way of simply oxidizing fat without ATP production. The physiological significance is discussed in slide 10.3.8.
| 6.3.2 |
The uncoupling action of dinitrophenol |
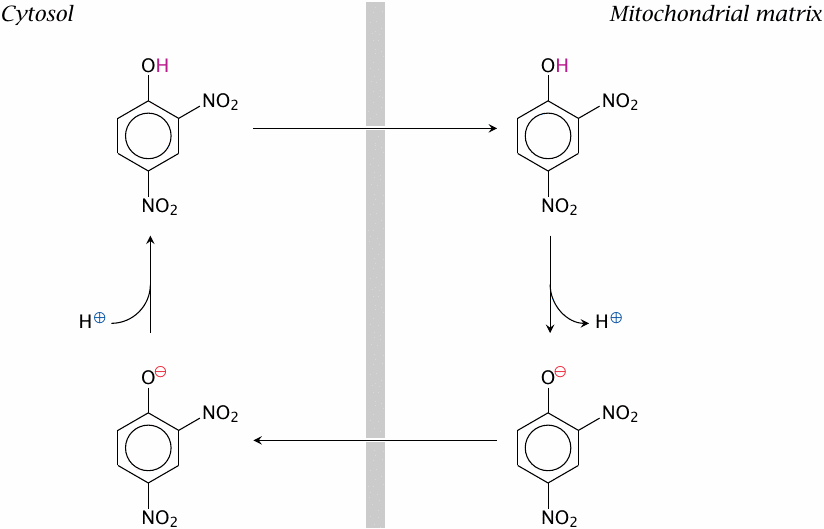
The synthetic compound dinitrophenol can diffuse across the inner mitochondrial membrane in both its protonated and unprotonated form. It can therefore carry protons into the mitochondrion, thereby dissipating the driving force for ATP synthase.29 Just like uncoupling proteins do in brown fat tissue, dinitrophenol will induce the burning of fat or other substrates and the production of heat—but in the mitochondria everywhere, not just in brown fat tissue. In the 1930s, dinitrophenol was used as a drug for losing excess body weight. It worked, too, but cases of fatal hyperthermia and other side effects caused the speedy discontinuation of this use. Wikipedia reports that the drug remains popular among bodybuilders, however, which seems of a piece with other reckless self-medication practices among the followers of this cult.
| 6.3.3 |
The Racker experiment: bacteriorhodopsin can drive ATP synthase |
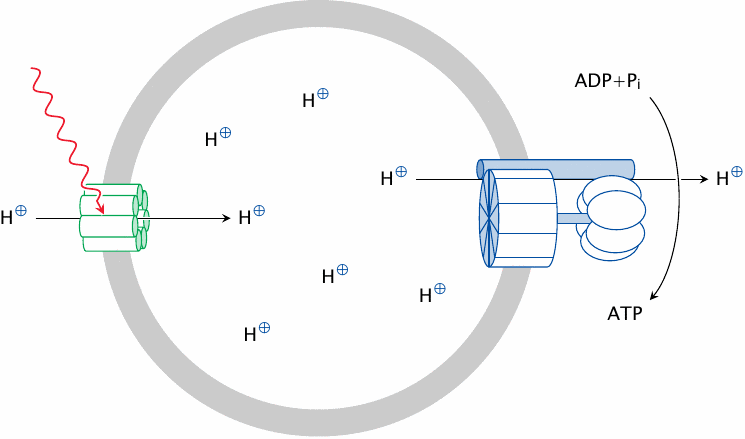
The effects of uncouplers show that electron transport can occur in the absence of ATP synthesis. On the other hand, ATP synthesis will occur in the absence of electron transport if a proton gradient is sustained in some other way. This was elegantly demonstrated by Ephraim Racker, who incorporated ATP synthase into liposomes along with bacteriorhodopsin, a membrane protein from the halophilic (that is, salt-loving) bacterium Halobacterium halobium.
Bacteriorhodopsin is a very unusual protein that functions as a light-driven proton pump: just shining light on it makes it pump protons across the membrane. In our experiment, illuminating the sample will make bacteriorhodopsin pump protons into the liposome. This will crank the ATP synthase and make it synthesize ATP from ADP and ionic phosphate.
Note that the orientation of both proteins shown here is inside-out relative to that found in their natural host membranes. Therefore, protons will here accumulate on the inside, and ATP synthesis proceed on the outside; this is the reverse of the situation in vivo.
The theoretical significance of these experimental findings is that, although the electron transport chain and ATP synthase reside in the same membrane and in close proximity, the proton gradient is the only required functional link between them. The electron transport chain generates the proton gradient, whereas ATP synthase puts it to work and thereby dissipates it. Because of this clear distinction, we can safely examine these two functions separately from each other.
| 6.4 |
Molecules in the electron transport chain |
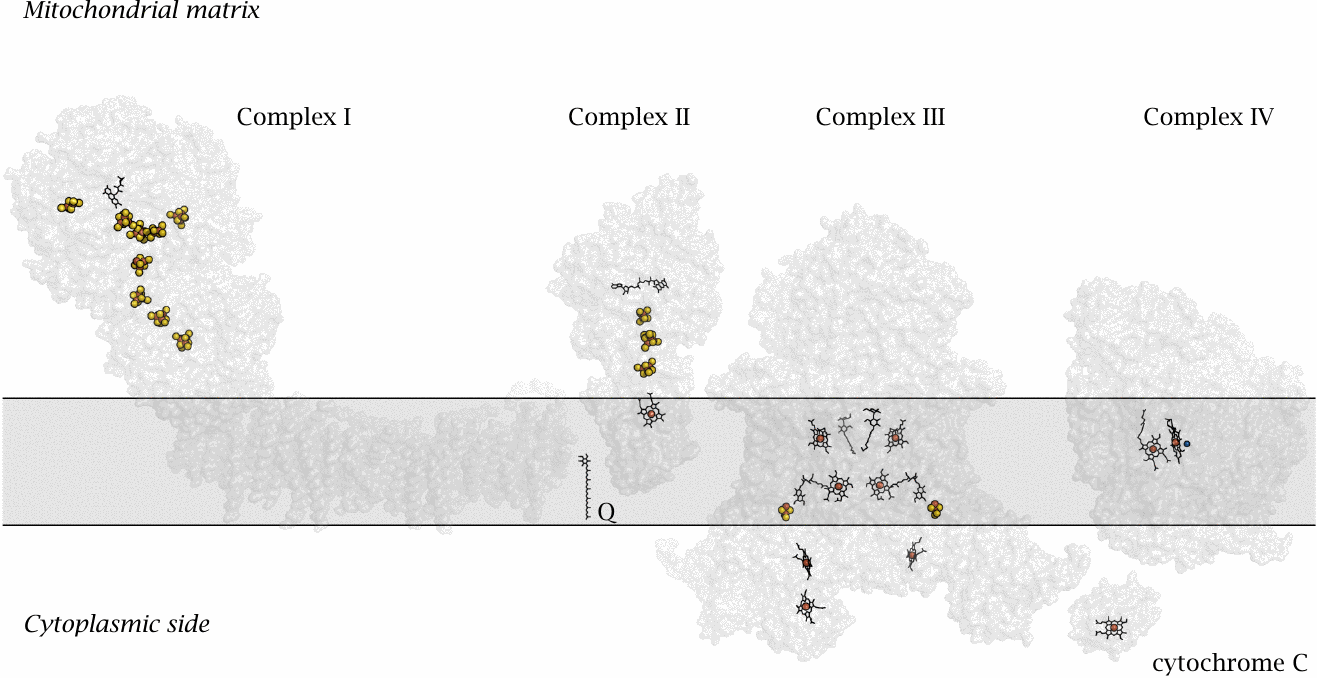
This slide shows the structures of the four respiratory chain complexes that form the respiratory chain.30 The gray rectangle represents the inner mitochondrial membrane. Among the redox cofactors, yellow and red blobs represent iron sulfur clusters. Organic rings (black) with red balls (iron atoms) in the center are hemes; other organic rings are flavins or ubiquinone (Q). The blue ball next to one of the hemes in complex IV is the copper ion in its active site. Each of the four complexes has a specific role in the electron transport process:
- 1.Complex I accepts hydrogen from NADH + H+and is therefore also called NADH dehydrogenase. The NADH is oxidized back to NAD+ and thereby readied for the next round of reduction in the TCA cycle or by pyruvate dehydrogenase. The hydrogen is split into electrons and protons. The electrons travel along a string of redox cofactors that traverses the entire protein complex and are then transferred to the small, membrane-resident carrier molecule known as ubiquinone or coenzyme Q , which passes them on to complex III. Powered by this electron migration, complex I ejects four protons across the membrane.
- 2.Complex II accepts hydrogen from FADH2, which was reduced by succinate. It was mentioned in slide 5.4.3 that complex is identical with succinate dehydrogenase, which drives home the point that the two pathways are really functionally one. The electrons are again transferred to coenzyme Q; however, no proton extrusion occurs at complex II.31
- 3.Complex III reoxidizes coenzyme Q and expels more protons. According to the coenzyme Q cycle model presented below, four protons are being expelled at this stage for each pair of electrons transported, but in some sources the number of protons expelled is given as two; this illustrates that there still is some uncertainty about the mechanistic details. Having performed their work at complex III, the electrons are delivered to the small electron carrier protein cytochrome C.
- 4.Complex IV accepts the electrons from cytochrome C and is accordingly also called cytochrome C oxidase. The electrons are transferred to oxygen, and the considerable free energy associated with this electron transfer step is used to expel up to four protons from the mitochondrial matrix.
Electrons do not occur in free form but are always part of molecules or ions.32 Therefore, to make electrons flow along the prescribed path along complexes I–IV, these proteins must provide functional groups that are able to accept and donate electrons. These groups must be closely spaced, within a few Angstroms of each other, to allow for efficient electron transfer. Furthermore, to persuade the electrons to flow in the right direction, the successive transitions must be exergonic, that is, their free energy (ΔG) must be negative.
In the figure above, you can see a multitude of redox cofactors, neatly spaced along the protein molecules, that function as “stepping stones” for the migrating electrons. These prosthetic groups fall into various structural classes.
| 6.4.1 |
Iron-containing redox cofactors |
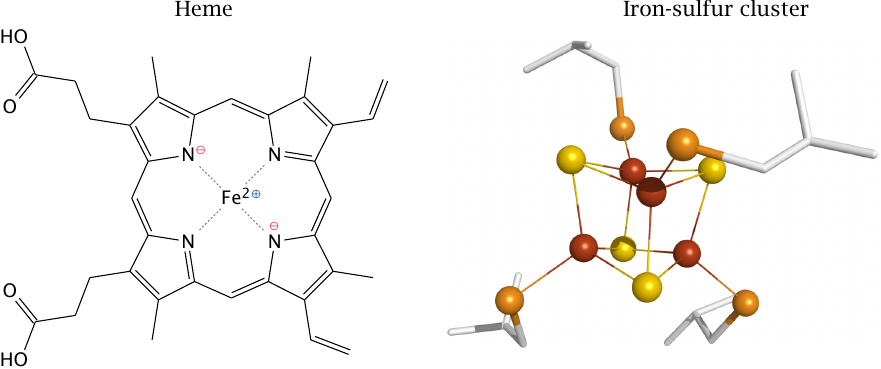
Most of the redox cofactors in the respiratory chain are hemes and iron-sulfur clusters, both of which contain iron ions. Hemes are tetrapyrrol rings that hold a single central iron ion. This iron ion can adopt different oxidation states, mostly Fe2+ and Fe3+, although Fe4+ occurs with one of the hemes in complex IV.33
In iron-sulfur clusters, it is again the iron that accepts and donates electrons by alternating between different oxidation states. Each iron ion is held in place by four sulfur atoms, which either belong to cysteine side chains (orange) or are free sulfide ions (S2−; yellow). The two types of sulfurs may occur in various numbers and proportions, which results in iron-sulfur clusters of different size.
The pyrrole rings or sulfur atoms do not only keep the iron ions in place but also modulate their redox potentials. These potentials are further tweaked by the specific molecular environment of each cofactor, in such a way as to enable the electrons to flow from one cofactor to the next.
| 6.4.2 |
Flavin-containing redox cofactors |
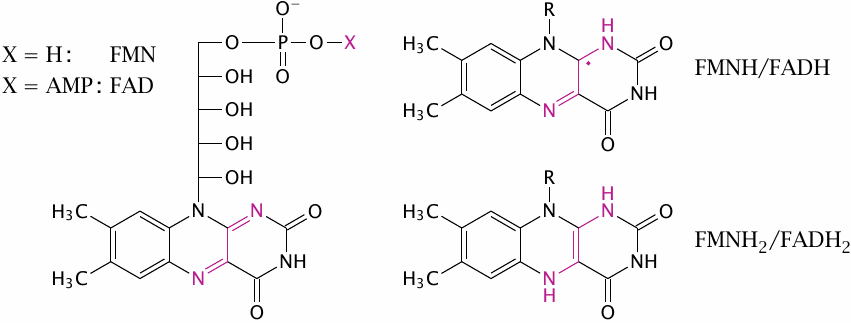
The flavin nucleotides flavin adenine dinucleotide (FAD) and flavin mononucleotide (FMN) can occur in three different states of reduction, which differ by single electrons. Unlike NAD, which can accept or donate electrons only in pairs, flavins can accept or yield electrons one at a time. Therefore, flavins can buffer the electron flow between NAD and iron-containing redox cofactors, and this is why the very first cofactor that accepts the electrons from NADH in complex I is indeed an FMN molecule.34
In addition to the stationary redox cofactors that occur within complexes I–IV, there are two electron carriers that are not tightly associated with one individual complex but function as shuttles between them:
- 1.Ubiquinone or coenzyme Q. This coenzyme contains a quinone group. It carries electrons, as hydrogen, from complexes I and II to complex III. It also contains a long hydrophobic polyisoprene tail, which confines it to the hydrophobic interior of the membrane. Like flavins, ubiquinone can transfer electrons singly or in pairs; this is important in the coenzyme Q cycle (see slide 6.6.3).
- 2.Cytochrome C. This is a small protein that again contains a heme. It is located at the outer surface of the inner mitochondrial membrane and shuttles electrons between complex III and complex IV.35
| 6.4.3 |
The respiratory chain generates reactive oxygen species as by-products |
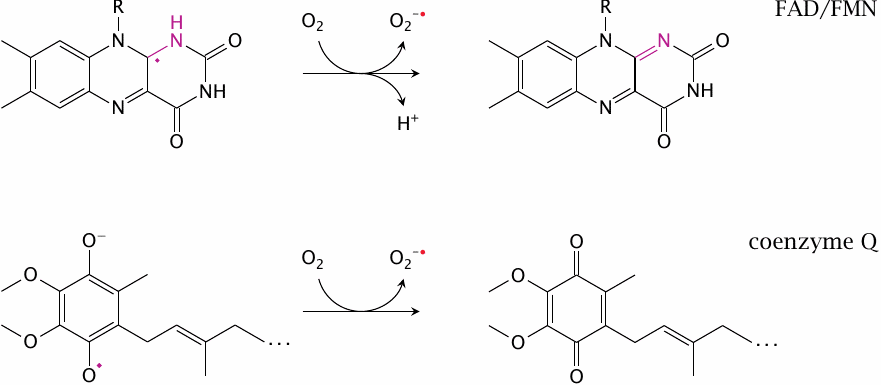
Several redox cofactors in the respiratory chain are prone to side reactions with molecular oxygen, which produce superoxide (O2•−) and other reactive oxygen species, that is, partially reduced forms of oxygen. These have the potential to damage cellular membranes and macromolecules and must be scavenged. This topic is discussed further in chapter 18.
| 6.5 |
The energetics of electron transport |
In discussing the driving forces of electron transport above, we have referred to both the free energy and the redox potential. Before considering the energetics of the respiratory chain in more detail, we will briefly review how exactly these two physical terms relate to one another.
| 6.5.1 |
Redox reactions can be compartmentalized to produce a measurable voltage |
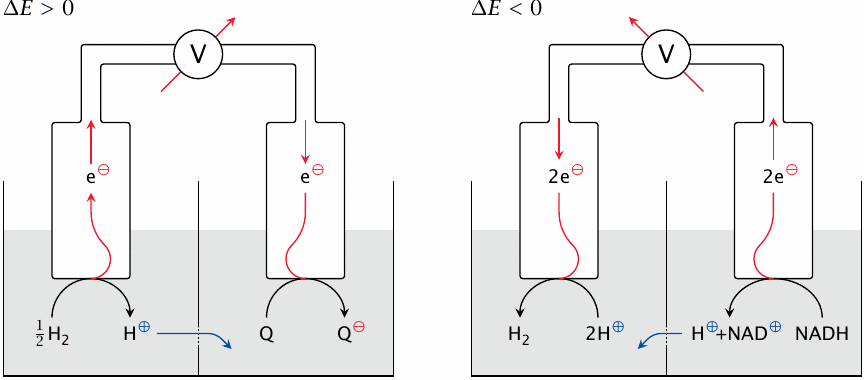
This slide illustrates the experimental setup for measuring the redox potential of an electron carrier. Left panel: coenzyme Q withdraws electrons from the standard hydrogen electrode, which by definition gives it a positive redox potential (ΔE). Right: NADH pushes electrons toward the standard electrode, making its ΔE negative.
In the experimental setup, the molecule of interest and a reference solute are contained in two adjacent buffer-filled chambers. Platinum electrodes are immersed in both solutions and connected through a voltmeter (V). As electrons are withdrawn from the solute in one chamber and delivered to the other, the voltmeter indicates the direction and magnitude of the potential difference. Protons and other ions can flow across a salt bridge between the chambers so as to preserve electroneutrality. In order to allow the flow of ions but prevent mixing of the chamber contents by convection, this hole is covered with a porous membrane or plugged with agar.
The reference solute commonly used in chemistry is H2, equilibrated with hydrogen gas at 1 atm above the solution. The corresponding oxidized form, H+, is adjusted to 1 mol/l or pH 0. The immersed platinum electrode not only conducts electrons but also serves as a catalyst for the interconversion between H2 and H+.
The potential of a redox carrier measured against this electrode is defined as its standard redox potential or ΔE0. For biochemical purposes, the standard electrode solution is buffered at pH 7 rather than pH 0, and the redox potentials measured against this electrode are referred to as ΔE0′. A pH of 7 is just as arbitrary a reference point as pH 0, but we will stick with it because the textbooks do so, too.
| 6.5.2 |
The redox potential (ΔE) is proportional to the free energy (ΔG) |
| ΔG | ≡ | \(\frac{\text{energy}}{\text{moles (number of molecules)}}\) | |
| ΔE | ≡ | \(\frac{\text{energy}}{\text{charge transferred}}\) | |
| ΔG | = | \(\frac{\text{energy}}{\text{charge transferred}} \; \times \; \frac{\text{charge transferred}}{\text{moles}}\) | |
| ΔG | = | \(\Delta E \; \times \; \frac{\text{charge transferred}}{\text{moles}}\) | |
| therefore | |||
| ΔG | = | \(- \Delta E \times n \times \text{F}\) | (6.1) |
From the previous slide, it is clear that electrons will flow spontaneously from one redox cofactor to another if the corresponding ΔE is positive. We also know that reactions proceed spontaneously if their ΔG is negative. The two parameters are directly related to one another according to equation 6.1. Either one is therefore sufficient to describe the energetics of the reaction; the reason why redox potentials are more commonly used in this context is that they can be measured more directly than ΔG.
In the equation, ΔE is the difference in the redox potentials between two cofactors. The parameter n is the number of electrons transferred in the reaction; for example, NADH feeds two electrons at a time into the chain, which means that n equals two for this reaction. In contrast, heme typically accepts and donates single electrons, which means that n=1. The F in the equation is Faraday’s constant, which tells us how many units of charge are carried by one mole electrons (96,500 coulombs/mol).36 One can think of a cofactor’s redox potential as its affinity for electrons—the higher it is, the more strongly the cofactor will attract electrons.37
| 6.5.3 |
Redox potentials and free energies in the respiratory chain |
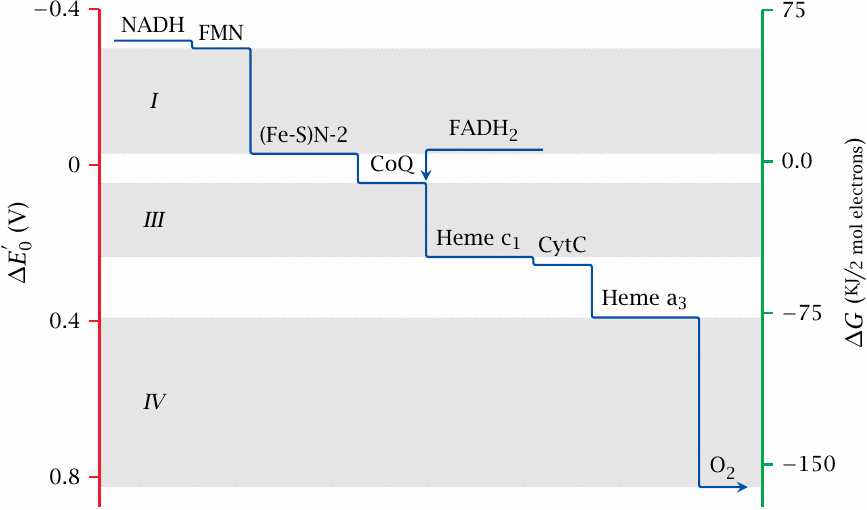
This slide shows the redox potentials, and the corresponding free energy levels, of some selected electron carriers in the respiratory chain. The lowest potential is found with NAD+, in keeping with its position at the start of the transport chain. The next carrier in sequence, FMN, is part of complex I. It has a slightly higher potential than NADH and is therefore able to accept its electrons. The redox potential increases continuously along the respiratory chain to reach its highest value at oxygen, which therefore has the highest affinity for the electrons and gets to keep them. Reduced oxygen, which recombines with protons to yield water, thus is the end product of respiration.
The iron-sulfur cluster N2, which occupies the lowermost position within complex I as shown in slide 6.4, has a significantly higher potential than the FMN. This step in potential corresponds to a significant amount of free energy that is released at some point within complex I as the electrons travel through it from FMN toward N2. Complex I uses this energy to expel protons from the mitochondrion, against their concentration gradient. Major steps in potential that drive proton expulsion also occur within complex III and complex IV.
Only minor steps of potential occur in the delivery of electrons from complex I to complex III via coenzyme Q, and between complexes III and IV via cytochrome C. Likewise, with complex II, the potentials of both entry and exit points must fall into the narrow interval between FADH2 and coenzyme Q, which means that very little energy is released as electrons traverse this complex. Such minor steps in redox potential suffice to jog the electrons along, but they are too small to contribute to proton pumping.
| 6.6 |
Interfacing different types of electron carriers |
In addition to their specific redox potentials, which establish the general direction of electron flow, the redox cofactors in the respiratory chain also differ in two other important aspects:
- NADH, FADH2, FMNH2 and coenzyme Q carry both electrons and protons—that is, hydrogen. In contrast, the hemes and the iron-sulfur clusters carry only electrons.
- NAD+ can only accept and donate pairs of electrons, whereas the hemes and iron-sulfur clusters can only accept and donate single electrons.
The switch from the two-electron carrier NADH to the one-electron carrying Fe–S clusters within complex I is negotiated by FMN, which, as discussed above, can accept or donate electrons both pairwise and singly.
| 6.6.1 |
The first two redox steps in complex I |
| NADH+H++FMN | ⟶ | NAD++FMNH2 | (6.2) |
| FMNH2+FeIII–S | ⟶ | FMNH•+H++FeII–S | (6.3) |
| FMNH•+FeIII–S | ⟶ | FMN+H++FeII–S | (6.4) |
After accepting H2 from NADH + H+ (equation 6.2), FMNH2 donates the electrons one by one to the first Fe–S cluster (equations 6.3 and 6.4), adopting a sufficiently stable radical form between these two transfers. The electron transfer between FMNH2 and Fe–S also illustrates what happens if an electron-only carrier is reduced by a hydrogen carrier: The protons are simply shed into the solution.
| 6.6.2 |
The reduction of coenzyme Q involves protons and electrons |
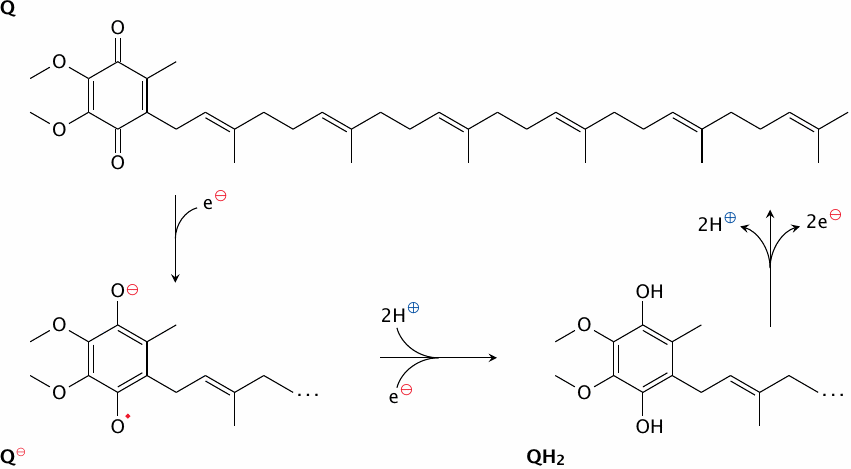
Hydrogen carriers may also be reduced by electron carriers. This happens with coenzyme Q, which is reduced by the iron sulfur cluster N2 in complex I. In this case, protons are taken up from the solution, but only in the second reduction step:
| FeII–S+Q | ⟶ | Q−•+FeIII–S | |
| FeII − S+2H++Q−• | ⟶ | QH2+FeIII–S |
Hydrogen carriers alternate with electron-only carriers at several points in the chain. This means that electrons are stripped of their protons and rejoined by protons again repeatedly during transport. Where protons are stripped off, they may be preferentially released at the cytosolic side, whereas uptake of protons may preferentially occur on the mitochondrial side. This would account for some, but not all of the proton translocation occurring in the respiratory chain.
As an example of of the foregoing, we will have a look at the (in)famous ubiquinone cycle. Ubiquinone (or coenzyme Q) is a hydrogen carrier; like FAD and FMN, it can carry two electrons but can accept and donate them one at a time.
| 6.6.3 |
The Q cycle (criminally simplified) |
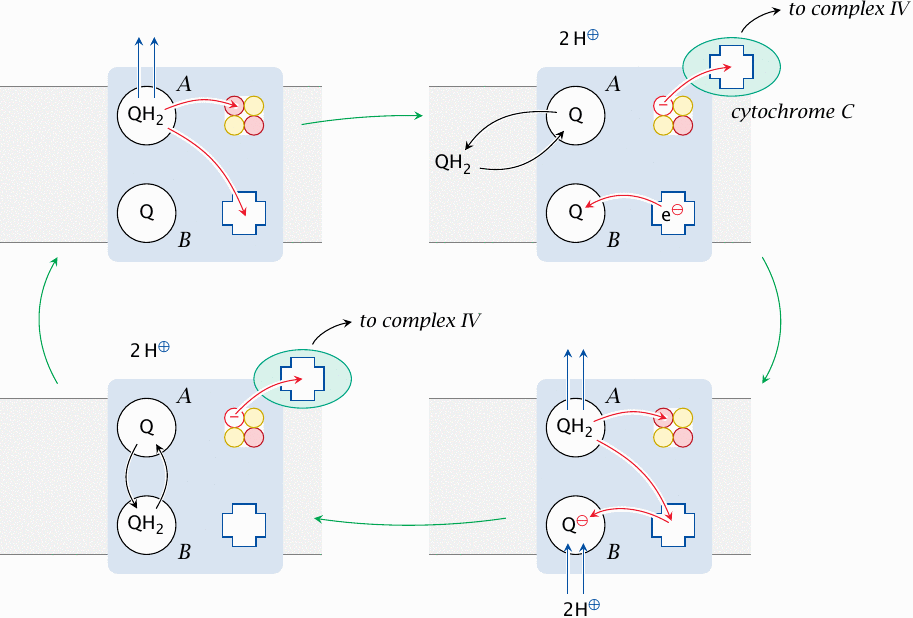
The Q cycle or ubiquinone cycle runs within complex III, which accepts reduced ubiquinone from the surrounding membrane. Complex III has two binding sites for ubiquinone, and both of them are occupied while the cycle runs; we will here call them A and B. The ubiquinone cycle goes through the following stages, starting at the top left:
- 1.At the outset, a reduced ubiquinone (QH2) is bound to site A, and an oxidized one (Q) is bound to site B. The protons of QH2 are now stripped off and expelled to the cytosolic side. The electrons part company and migrate to two different electron carrier groups within complex III; one of these is an iron-sulfur cluster, whereas the other is a heme.
- 2.The iron sulfur cluster donates its electron to cytochrome C, while the heme transfers its electron to the second molecule of ubiquinone in site B. The ubiquinone molecule in site A, now oxidized, trades places with another one in the surrounding membrane that was reduced in the preceding steps of the respiratory chain.
- 3.The protons and electrons of the new QH2 in site A are abstracted and split as in the first step. The heme passes on its electron to coenzyme Q in site B. Now completely reduced, the coenzyme Q picks up two protons from the mitochondrial matrix to form QH2.
- 4.The electron that had been transferred to the Fe–S cluster is donated to cytochrome C. The Q in site A trades places with QH2 in site B, which completes the cycle.
According to this scheme, with each molecule of ubiquinone reduced in the respiratory chain, the two protons it carries are expelled into the cytosol, and two additional protons are taken up from the mitochondrial matrix and expelled into the cytosol as well. Therefore, complex III uses ubiquinone as a prosthetic group to facilitate the movement of protons across the membrane.
If you compare the outline of the ubiquinone cycle given here to the description in your textbook, you might find the similarity somewhat remote. In reality, as you can see in slide 6.4, complex III contains several more redox co-factors that act as intermediate stepping stones in the electron transfer steps outlined above. They have been skipped here for simplicity.
| 6.6.4 |
Reduction of oxygen by cytochrome C oxidase (complex IV) |
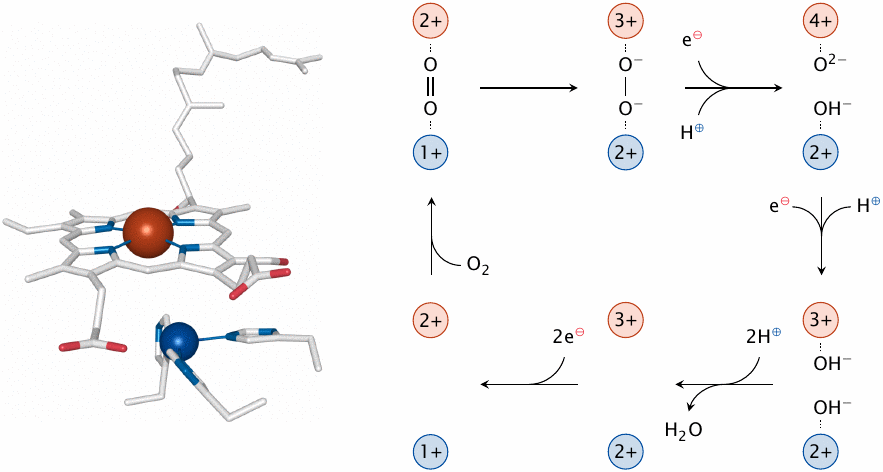
Cytochrome C is a small hemoprotein that shuttles electrons from complex III to complex IV. The latter complex, which is also known as cytochrome C oxidase, completes the transfer of electrons by delivering them to oxygen. In the process, it pumps some more protons out of the mitochondrial matrix. The reduction of oxygen is the trickiest step in the entire respiratory chain, as it takes a full four electrons to reduce molecular oxygen (O2) all the way to two molecules of water. Since cytochrome C delivers the electrons to complex IV one at a time, the reduction will involve partially reduced oxygen species. As noted above, partially reduced oxygen species are reactive and toxic when let loose upon the cell, so their premature release from cytochrome C oxidase must be minimized.
Cytochrome C oxidase does its best to control this problem by binding oxygen tightly and reducing it swiftly. The oxygen molecule is clamped in the active site between the iron of a heme and a copper ion, which is coordinated by three histidine residues (left). Both metal ions also function as redox cofactors in the reduction. Each of them advances one electron to the oxygen, which is thereby reduced to peroxide, using one electron from each metal ion. Uptake of an electron delivered by cytochrome C and abstraction of a further one from the iron fully reduces both oxygen atoms. Uptake of protons generates first hydroxide and then water, which is released. Iron and copper are subsequently restored to their original oxidation levels further electrons obtained from cytochrome C.
| 6.7 |
How is electron transport linked to proton pumping? |
- Some redox steps in the ETC are coupled to proton binding and dissociation, which may occur at opposite sides of the membrane. Example: Coenzyme Q cycle at complex III
- Redox steps that do not involve hydrogen directly need a different mechanism in order to contribute to proton pumping. Example: Sequence of iron-sulfur clusters and hemes in complex IV
As pointed out above, some of the protons that undergo expulsion from the mitochondrion are accepted from the hydrogen carriers NADH and ubiquinone and travel together with electrons for a part of the journey. However, at some point they must part company, and the protons must be expelled, whereas the electrons are retained. Also, more protons are being expelled than can be accounted for by the hydrogen carriers. This is obvious with complex IV, which does not interact with any hydrogen carriers at all yet expels up to four protons for each pair of electrons accepted. So, there must be mechanisms that extract energy from the transfer of proton-less electrons and apply it towards the expulsion of electron-less protons. How does this work?
| 6.7.1 |
Linking electron movement to proton pumping: A conceptual model |
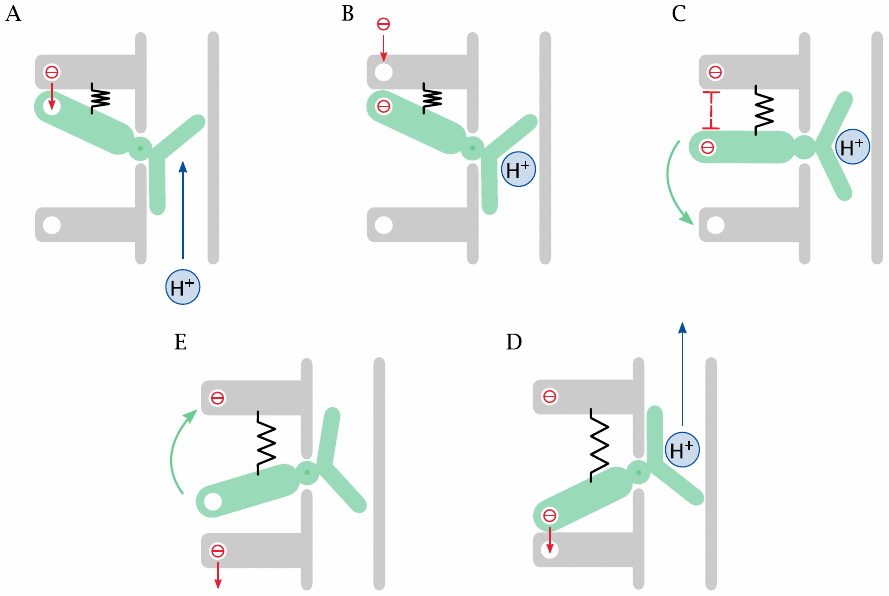
The experimental evidence on this point is still tentative, and inasmuch as they are understood, the emerging mechanisms are quite complex. Therefore, instead of trying to describe them faithfully, this slide presents a simplified conceptual model to provide an idea of how things might work.
The basic idea is that capture and release of electrons cause conformational changes to a protein. This is entirely analogous to conformational changes caused by allosteric effectors binding to enzymes, or by phosphate groups bound to cytoskeletal proteins such as the myosin light chain. An electron carries a charge, a charge causes a field, and a field creates forces that act on charged residues on the protein; thus, in principle, it is not hard to imagine how migrating electrons can cause conformational changes.
In our conceptual model, a spring-loaded valve controls the proton conduit. The lever of the valve carries an electron-transporting cofactor (a heme or FeS-cluster). This cofactor receives an electron from another cofactor upstream (A), which then becomes occupied by the next electron (B). Electrostatic repulsion moves the valve (C), such that the proton is translocated and the electron can jump to the next cofactor downstream (D). The extended spring—which is a metaphor for conformational strain—then returns the valve to its original position (E).
| 6.7.2 |
Stoichiometry of proton ejection |
It is commonly stated that approximately ten protons are ejected for each pair of electrons abstracted from NADH, such that four protons are ejected at each of complexes I and IV, and 2 at complex III.38 Complex II does not eject any protons but just abstracts them from FADH2 and passes them on to ubiquinone. If you look at slide 6.5.3, you will notice that the difference in the redox potentials of FAD and ubiquinone is rather small. Consequently, the amount of free energy associated with the transfer of electrons from FAD to ubiquinone is too small to permit the performance of work against the proton gradient.
| 6.8 |
ATP synthesis |
Most of the ATP that results from complete oxidative degradation of glucose is synthesized only after the substrate has already vanished in the form of CO2 and H2O. At this stage, the entire available energy is stored in the so-called proton-motive force across the inner mitochondrial membrane. ATP synthesis is powered by the protons that yield to this force and are pulled back by it into the mitochondrion.
| 6.8.1 |
Proton pumping creates both a concentration gradient and a membrane potential |
| \(\Delta G_{\text{concentration}}\) | = | \(RT \times \text{ln}\,K = 6\,\mathrm{\frac{kJ}{mol}}\) | (6.5) |
| \(\Delta G_{\text{potential}}\) | = | \(\Delta\psi \times n \times \text{F} = 15\,\mathrm{\frac{kJ}{mol}}\) | (6.6) |
The proton concentration in the cytosol is approximately ten times higher than that in the mitochondrial matrix. While this creates a significant significant driving force, the larger contribution to the overall proton-motive force comes from the electrostatic membrane potential across the inner mitochondrial membrane. Like the proton concentration gradient, this electrical potential is a direct consequence of the proton pumping: Each proton ejected leaves one negative charge behind inside the mitochondrion.
In a fully energized mitochondrion, the membrane potential amounts to approximately ~150 mV.39 According to equation 6.6, this potential confers a free energy of approximately 15 kJ/mol to each proton, whereas equation 6.5 indicates a contribution of only 6 kJ/mol from the concentration gradient. In summary, therefore, the proton-motive force is dominated by the membrane potential.
| 6.8.2 |
Structure of ATP synthase |
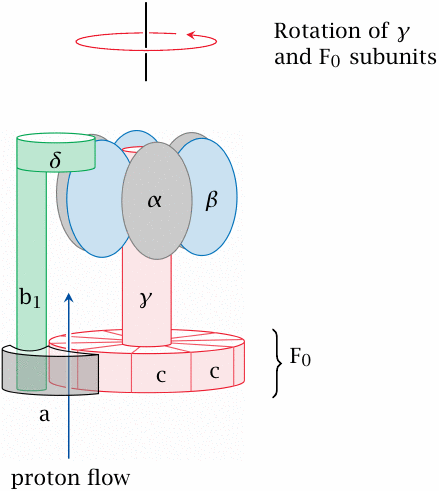
This complex and fascinating molecule is both an enzyme and a molecular motor.40 The slide shows a side view. Ten identical c subunits are arranged like pie slices; the whole cylindrical pie is referred to as the F0 subunit. It and the a subunit are embedded in the inner mitochondrial membrane, whereas the other subunits of the molecule protrude into the mitochondrial matrix.
The F0 and the γ subunit (both shaded in red) rotate relative to all other subunits. The γ stalk therefore rotates within and rubs against the bushing formed by the six α and β subunits. The rotation is driven by the flow of protons that occurs at the interface of the a and F0 subunits.
| 6.8.3 |
The binding-change model of ATP synthase catalysis |
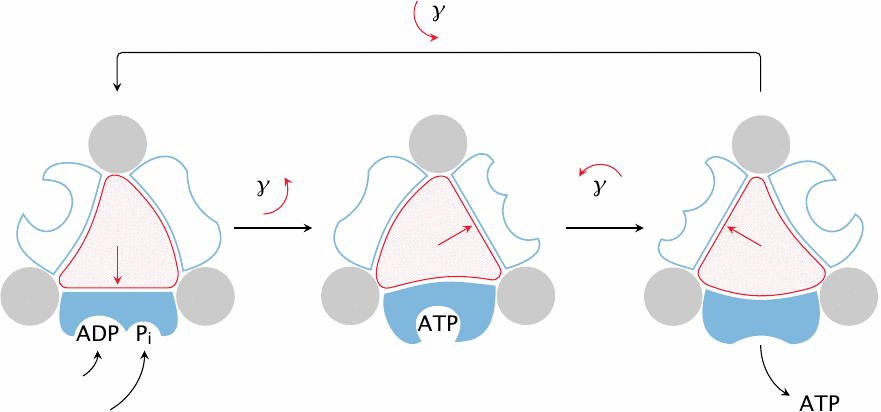
The interaction of the rotating γ subunit with the static β subunits is crucial to ATP synthesis. Because of the asymmetric shape of the γ subunit, its rotation imposes cyclic conformational changes upon the α and β subunits that surround it. The β subunit, which contains the active site of the enzyme, extracts mechanical work from these conformational changes and ultimately converts it into the chemical energy contained in ATP.
How does the β subunit convert mechanical into chemical energy? Strictly speaking, it doesn’t—it turns out that the isolated β-subunit can create ATP from ADP and ionic phosphate all by itself. In doing so, the β subunit adopts two distinct conformational states. In the first state, it binds ADP and phosphate. Once both are bound, β transitions to the second state, which binds ATP with exceptionally high affinity but no longer binds ADP and phosphate. Formation of several avid but non-covalent bonds between β and ATP provides the energy that is needed to create the new, energy-rich phosphate anhydride bond in ATP.
With the isolated β subunit, we have at this point reached a dead end—ATP is bound so avidly as to never be released, which means that no further turnover can occur. It is at this stage that, in the intact enzyme, the γ subunit comes into play. Rotation of γ forces another change of conformation upon β that in turn kicks the ATP out of the active site. The force imposed by γ on β must be so strong as to overcome and offset the large binding energy that ties the ATP to β. In summary, therefore, the synthesis of ATP proceeds spontaneously inside β, and the energy of rotation is applied to force out the avidly bound ATP and thus prime β for the next round of catalysis.
| 6.8.4 |
How does proton flux drive ATP synthase? |
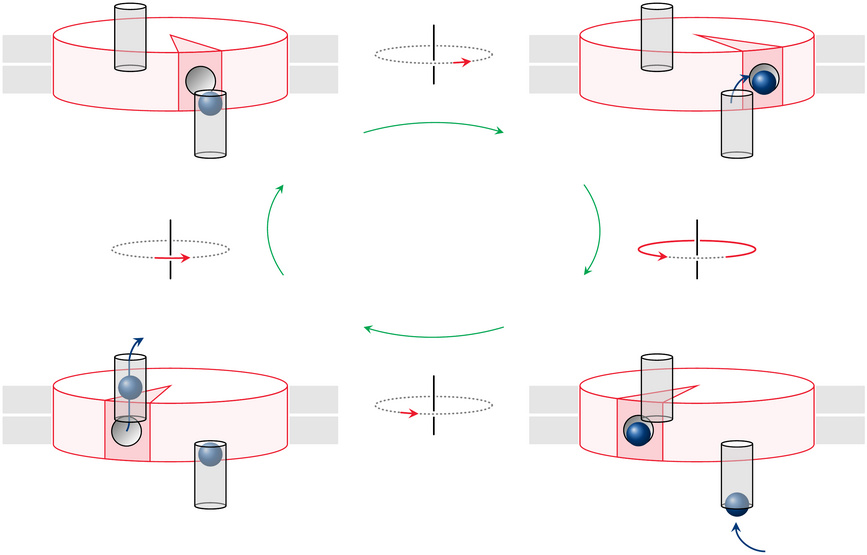
The last remaining puzzle is how the proton flux actually causes the moving parts of the enzyme to rotate. As shown in slide 6.8.2, the proton flux passes between the a subunit and the F0 subunit, which contains 10 identical c chains arranged in a pie-slice fashion; for simplicity, only one c chain is highlighted in the current slide.
The two gray cylinders in this cartoon are proton conduits contained within the a subunit; the remainder of the a subunit is not shown. The proton conduits span the outer and the inner membrane leaflet, respectively, but they do not meet; it is the rotating F0 disk that mediates the flow of protons between them. To this end, each c chain has a strategic aspartate residue that faces the surrounding lipid membrane and can reversibly accept a proton.
In the top left of the figure, the aspartate (shown as a little groove) of the highlighted c subunit is about to accept a proton from the periplasmic space41 via the corresponding conduit. In the next frame, the disk has moved a bit and accepted the proton; it then goes around by almost a full turn, until it reaches the other conduit (bottom right). In the final frame, the proton has left the disk and is on its way to the mitochondrial matrix, while the c subunit is about to move on and pick up then next proton.
There is indeed evidence that agrees with this model; for example, the strategic aspartate on the F0 disk is alternatingly accessible from the two opposite sides of the membrane. However, while it seems simple and elegant, this model has one fundamental shortcoming: While it tells us how rotation of ATP synthase can dissipate the proton gradient, it does not explain how ATP synthase manages to derive any torque from this process, so that it can perform work against resistance. More specifically, what makes the rotor keep going in the same direction instead of just oscillating back and forth between the two conduits? This would save it the trouble of performing work, while still permitting proton flux.42
| 6.8.5 |
Proton flux causes c chains to rotate within the F0 disk |
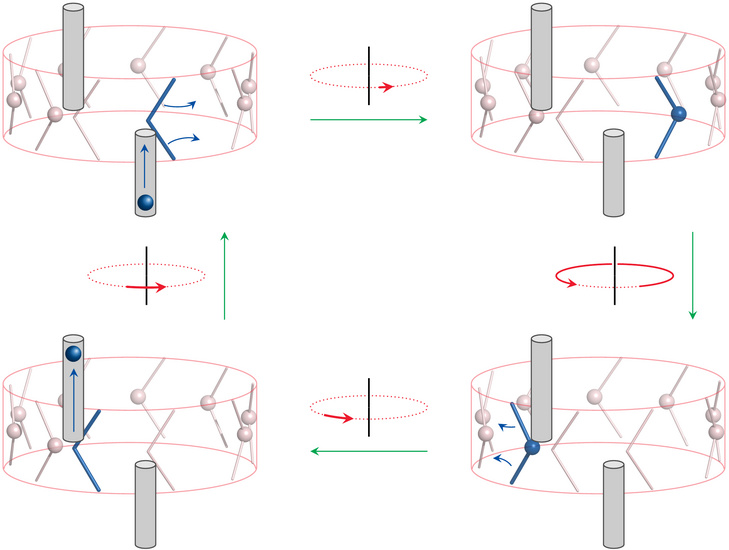
The absence of a flywheel effect that would help F0 move past dead spots means that proton flux and F0 rotation must be tightly coupled. This assumption is supported by the observation that the c chain undergoes a significant conformational change upon protonation or deprotonation [22]. The authors of the cited study proposed a functional model that is shown here in a simplified cartoon depiction.
One of the 10 c subunits is highlighted in blue, as is the proton carried by it. In the top left, this subunit is about to accept a proton from the cytosolic conduit. In the second frame, the proton has been accepted, and the c subunit has rotated about its own axis. The entire F0 disk then rotates by nearly a full turn, which brings our highlighted c subunit to the inward-connecting conduit. The aspartate now delivers its proton, whereupon the subunit swivels back about its own axis. During this transition, the aspartate holds on to the end of the conduit—that is, the stationary a subunit—and thus causes the entire F0 disk to rotate forward. This second rotation of the c subunit constitutes the “power stroke” of the engine.
The model implies that the number of protons transported per rotation is identical to that of the c subunits in F0. Intriguingly, ATP synthases in different organisms vary in their number of c subunits, which will directly affect the stoichiometric ratio of ATP synthesis to proton transport. It would be interesting to know whether there are complementary variations in the number of protons driven out per electron during electron transport. Otherwise, the different subunit stoichiometry of F0 should directly translate into a different ATP yield in the entire respiratory chain.
| 6.9 |
Auxiliary shuttles for the mitochondrial reoxidation of cytosolic NADH |
In slide 3.4.1, it was mentioned that, under aerobic conditions, the NAD+ converted to NADH in the cytosol by glyceraldehyde-3-phosphate dehydrogenase is re-oxidized in the respiratory chain. NADH itself, however, cannot pass the inner mitochondrial membrane, and in fact not even the more permissive outer membrane. How, then, is its oxidation accomplished?
It turns out that NADH is not translocated at all but is reoxidized, or dehydrogenated, in the cytosol. The hydrogen is then taken to the mitochondrion by other carriers. These shuttle system work in a somewhat roundabout manner, tying together several enzyme activities with specific transporters in the inner mitochondrial membrane.
| 6.9.1 |
A hypothetical malate-oxaloacetate shuttle |
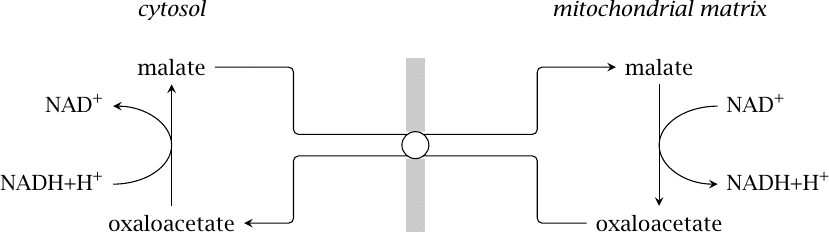
A simple but somewhat dubious shuttle is shown in this picture. Among the various mitochondrial exchange transporters that engage malate, there is one that can directly swap it for oxaloacetate [23]. This transporter has been found in the mitochondria of multiple mammalian organs, and under suitable conditions in vitro, it can sustain reoxidation of external NADH by isolated mitochondria [24].
The problem with this hypothetical shuttle is the ratio of NADH to NAD+, which in vivo is usually higher in the mitochondria than in the cytosol. This should crank the malate-oxaloacetate shuttle the wrong way, exporting NADH from the mitochondria rather than importing it. Therefore, until evidence of its operation within intact cells becomes available, this cycle cannot be assumed to be of major significance.
| 6.9.2 |
The malate-aspartate shuttle |
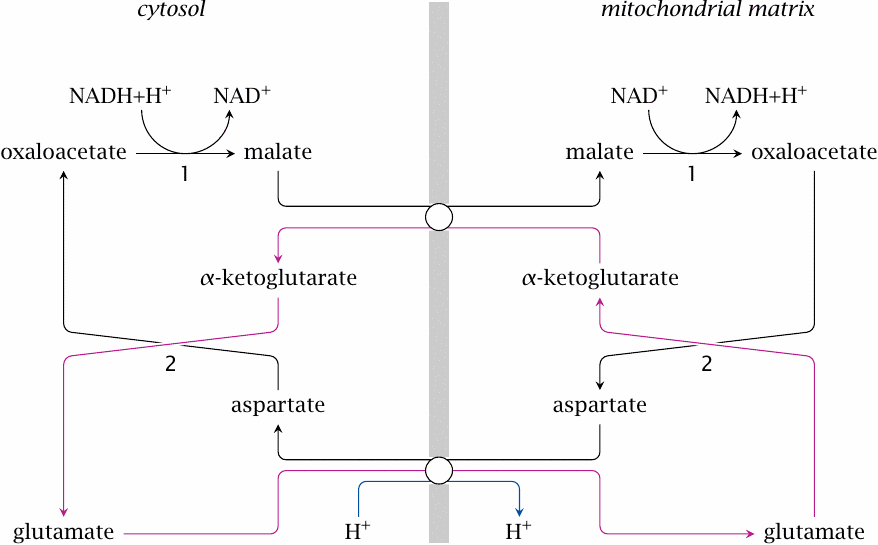
The malate-aspartate shuttle combines four substrates and two transporters with two enzymes, both of which are required on both sides of the membrane. In the cytosol, malate dehydrogenase (1) regenerates NAD+ by reducing oxaloacetate to malate, which is then exchanged for mitochondrial α-ketoglutarate. Inside the mitochondrion, malate is converted back to oxaloacetate, which is then transaminated by aspartate aminotransferase (2). This yields aspartate, which is exchanged for cytosolic glutamate, as well as α-ketoglutarate, which is exchanged for malate. Transamination is then reversed in the cytosol, which restores oxaloacetate and glutamate and closes the cycle.
While the malate-aspartate shuttle is more complex than the malate-oxaloacetate shuttle, it does have the advantage with respect to driving force: the glutamate-aspartate exchanger cotransports one proton with each molecule of glutamate, which means that the proton-motive force drives the cycle in the required direction [25].
The significance of this shuttle in vivo is supported by both experimental and clinical observations. Genetic defects of enzymes or carriers in the cycle cause lactic acidosis, that is, a pathological accumulation of lactic acid in the body, which indicates that the normal disposal of cytosolic NADH is disrupted. Similarly, pharmacological inhibition of aspartate aminotransferase with aminooxyacetate inhibits glucose oxidation and increases lactate levels [25,26].
| 6.9.3 |
The glycerophosphate shuttle |
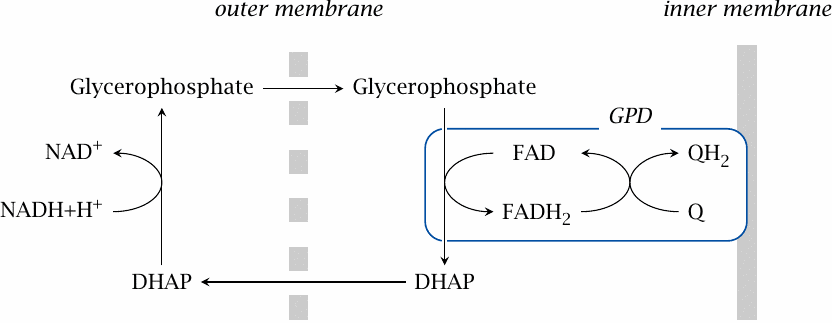
In the glycerophosphate shuttle, the hydrogen is never actually transported to the mitochondrion. Dihydroxyacetone phosphate serves as the intermediate hydrogen acceptor and is reduced in the cytosol to glycerophosphate by glycerophosphate dehydrogenase. Glycerophosphate traverses the outer mitochondrial membrane and is then reoxidized to dihydroxyacetone phosphate by a second glycerophosphate dehydrogenase (GPD). This enzyme is associated with the outer surface of the inner membrane, and it feeds the abstracted electrons directly into the respiratory chain at the level of coenzyme Q. Like succinate dehydrogenase, which also supplies electrons to the respiratory chain at the level of coenzyme Q, glycerophosphate dehydrogenase employs FAD is the coenzyme.
The glycerophosphate shuttle bypasses complex I in the respiratory chain and therefore induces ejection of four fewer protons from the cytosol. However, this shortfall is partially compensated for by the two protons that stay behind in the cytosol (or more accurately, the periplasmic space) when the electrons get abstracted from glycerophosphate. While slightly less energy-efficient than the malate-aspartate shuttle, this shuttle is certainly more straightforward, since it avoids all substrate transport across the inner mitochondrial membrane. In particular, it cuts out oxaloacetate, whose low concentration inside the mitochondrion probably forms the kinetic bottleneck of the malate-aspartate shuttle. It is interesting to note that the glycerophosphate shuttle is highly active in insect muscle, which has an extremely high ATP turnover during flight.
| 6.10 |
Regulation of the respiratory chain |
Most of the time and in most cells, the respiratory chain runs at rates that are substantially below the maximum. How is the flow rate of the respiratory chain controlled? In a healthy and not maximally exerted cell, there is much more ATP than ADP or phosphate, so that these become limiting for the flow. If ATP synthase is short of substrates, dissipation of the proton-motive force will slow down. The proton pumps will find it difficult to extrude more protons, and since electron transport and proton pumping are tied to one another, the dehydrogenation of NADH and FADH2 will slow down as well.
The flow rate of the respiratory chain also affects those of glycolysis and the TCA cycle. Both ATP and NADH participate in this regulation:
- A low consumption of ATP will result in its accumulation to higher levels. Many enzymes, including phosphofructokinase, are inhibited by ATP.
- Low activity of the respiratory chain causes NADH to accumulate, which slows down glyceraldehyde-3-phosphate dehydrogenase, pyruvate dehydrogenase, α-ketoglutarate dehydrogenase, and the NAD+-dependent isocitrate dehydrogenase.
It should be noted that mitochondrial respiration does not completely stall, even when no ADP is available as a substrate for ATP synthase. In this situation, the membrane potential across the inner mitochondrial membrane rises higher, which in turn makes the inner mitochondrial membrane more permeable to protons. This so-called proton leak is responsible for about 20% of the metabolic rate at rest. While several different transport proteins have been proposed to account for the proton leak [27], the most plausible mechanism is the futile cycle discussed in slide 6.10.3 below.
| 6.10.1 |
The two mitochondrial isocitrate dehydrogenases |
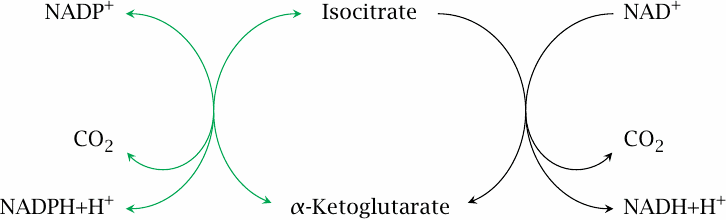
The above regulatory mechanisms are quite straightforward. There is, however, one remaining mystery. We have already noted that there are two forms of isocitrate dehydrogenase, one using NAD+ and the other NADP+ as the cosubstrate. While the NAD+-dependent form is inhibited by NADH and ATP, the NADP+-dependent form is not, and one might thus expect that it would go at full blast even when the demand for ATP is low and NADH is high. What is more, the NADP+-dependent enzyme is actually more highly expressed than the NAD+-dependent form. How, then, is the NADP+-dependent enzyme prevented from uncontrolled consumption of isocitrate, and why does it exist at all?
The answer to the first question is that, at least when demand for ATP is low, the NADP+-dependent isocitrate dehydrogenase reaction is close to equilibrium. This equilibrium is sustained by a high mitochondrial level of NADPH, which in turn is maintained by nicotinamide nucleotide transhydrogenase.
| 6.10.2 |
Nicotinamide nucleotide transhydrogenase couples hydrogen transfer with proton transport |
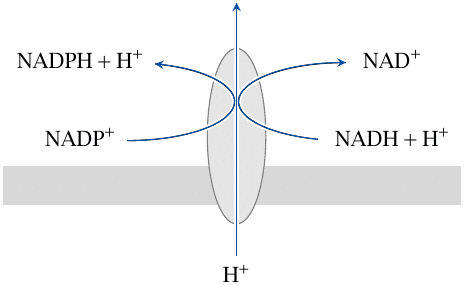
This remarkable protein, which is located in the inner mitochondrial membrane, is both an enzyme and a transporter. It reduces NADP+ to NADPH at the expense of NADH. As with ATP synthase, the enzyme reaction is coupled to the translocation of protons:
| NADH+NADP++H+out | ⟶ | NAD++NADPH+H+in |
Note that the transhydrogenase involves only mitochondrial NAD and NADP; the pools existing in the cytosol are unaffected.
| 6.10.3 |
At rest, transhydrogenase and the two isocitrate dehydrogenases form a futile cycle |
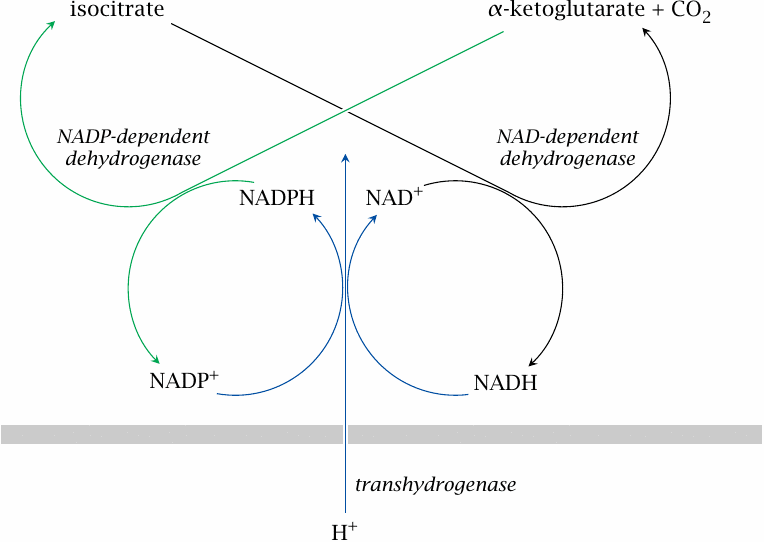
This slide and the following one show how the transhydrogenase may be integrated with the function and regulation of the TCA cycle and the respiratory chain [28].
When the demand for ATP is low, mitochondrial NADH and the proton-motive force will both be at high levels, which will cause the transhydrogenase to reduce NADP+ at the expense of NADH. Accordingly, the NADPH concentration will be high, which results in near-equilibrium conditions for the NADP+-dependent isocitrate dehydrogenase also. If the NADPH concentration is high enough, there would be a low net flux within an interesting futile cycle that involves both isocitrate dehydrogenases and the transhydrogenase, and the net effect of which is the influx of one proton in each round.43
| 6.10.4 |
When ATP demand is high, transhydrogenase turns into an auxiliary proton pump |
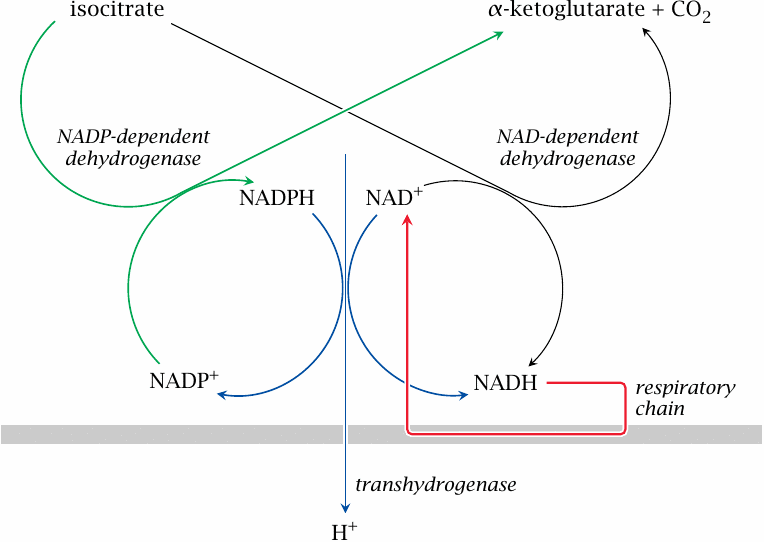
On the other hand, when the demand for ATP is high, the proton-motive force and the level of NADH will be lower. Under these conditions, the transhydrogenase should switch direction, now consuming NADPH to produce more NADH, which in turn will be consumed at a fast clip in the respiratory chain. This also means that transhydrogenase will work as an auxiliary proton pump, thus augmenting the proton-motive force and ATP synthesis.
What is more, the consumption of NADPH by transhydrogenase will topple the equilibrium of NADP+-dependent isocitrate dehydrogenase. Like the NAD+-dependent enzyme, it will now consume isocitrate. Due to the NADP+-dependent enzyme’s higher abundance, NADPH will be preferentially generated, with the benefit of an extra proton expelled by transhydrogenase.
Now this is a truly marvelous piece of engineering by Mother Nature, isn’t it? I’d say this is as close as it gets to intelligent design.
| 6.11 |
ATP yield of complete glucose oxidation |
The amount of ATP gained in the respiratory chain for each molecule of glucose degraded is large, but it cannot be calculated with complete precision and varies between different physiological states.
| 6.11.1 |
Theoretical ATP yield per molecule of glucose completely oxidized |
| Quantity | Intrinsic value | Per glucose |
| Accrued hydrogen | 10 NADH, 2 FADH2 | |
| Protons ejected | 10 per NADH, 6 per FADH2 | 112 |
| Proton-powered ATP synthase revolutions | 10 protons per revolution | 11.2 |
| ATP from ATP synthase | 3 per revolution | 33.6 |
| ATP from glycolysis | 2 | |
| GTP from TCA cycle | 2 | |
| Total | 37.6 |
The number of NADH molecules given here includes all molecules accruing in glycolysis, pyruvate dehydrogenase, and the TCA cycle. The numbers of protons pumped per molecule of NADH or FADH2 are based on the assumption that complexes I, III, and IV pump 4, 2, and 4 protons, respectively. GTP, which is formed in the succinate thiokinase reaction in the TCA cycle, is energetically equivalent to ATP.
| 6.11.2 |
Processes other than ATP synthesis that are powered by the proton gradient |
- Nicotinamide nucleotide transhydrogenase
- Uncoupling proteins; proton leak
-
Secondary active transport:
- ATP4−/ADP3− antiport
- phosphate/H+ symport
- amino acid/H+ symport
- pyruvate/H+ symport
The amount of ATP given in the preceding slide is a theoretical maximum. In reality, the ATP yield will be significantly lower, because some protons are used for purposes other than driving ATP synthase. Most importantly, some protons are needed for ATP transport. ATP synthesized in the mitochondrion must be exported to the cytosol, and ADP produced there has to get back in. This is accomplished by a special transporter protein in the inner mitochondrial membrane that exchanges ATP and ADP for each other. Since ATP carries one more negative charge than ADP (ATP4– vs. ADP3–), this exchange amounts to a net export of one negative charge, or to the net import of one positive charge per ATP. Moreover, ionic phosphate produced by cytosolic ATP cleavage also must return to the mitochondrion, which consumes another proton. These processes detract considerably from the theoretical efficiency of ATP synthesis.
The expenditure of extra protons on the transport of ATP, ADP and phosphate provides a clear benefit to the cell. It allows the transport of ATP and ADP against their concentration gradients. This enables the cell to maintain a high ATP/ADP ratio in the cytosol, which helps drive the ATP-consuming reactions there forward, whereas a higher ADP/ATP ratio in the mitochondria allows the ATP synthase to go at speed.