| 2 |
A primer on ionizing radiation and radioactivity |
This chapter is intended solely to explain some fundamental scientific concepts that will be used in later chapters; it does not go into any specifics on the atomic bombs purportedly dropped on Japan. Readers with the required scientific background may safely skip it.
| 2.1 |
Atoms and subatomic particles |
Radioactivity involves the building blocks of individual atoms, so this is where we will start our guided tour. Each atom has a nucleus, which contains one or more protons and zero or more neutrons, and it also has a shell, which contains electrons (Figure 2.1). The number of protons in the nucleus determines which chemical element the atom belongs to. The atoms of a given chemical element may, however, differ by the number of neutrons; atoms of the same element that also share the same number of neutrons belong to the same isotope. For example, hydrogen has three isotopes, each of which has one proton. Protium, the most abundant hydrogen isotope, has no neutrons; deuterium and tritium have one and two neutrons, respectively. Nuclei that share the same number of protons and neutrons are also said to belong to the same nuclide.19 This term is synonymous with ‘isotope’ but typically used when the focus is on the properties of atomic nuclei, rather than on specific chemical elements; for example, Figure 2.1 illustrates three different nuclides.
A common shorthand notation for the composition of a nuclide uses the symbol of the chemical element, for example H for hydrogen, prefixed with a subscript that indicates the number of protons and a superscript for the number of nucleons, by which we mean both protons and neutrons. For example, the isotopes of Hydrogen are 11H, 12H, and 13H, while the two major isotopes of uranium are 92238U and 92235U. Since the number of protons is also implicit in the element, the corresponding prefix is often omitted, as in 235U instead of 92235U or 3H instead of 13H.
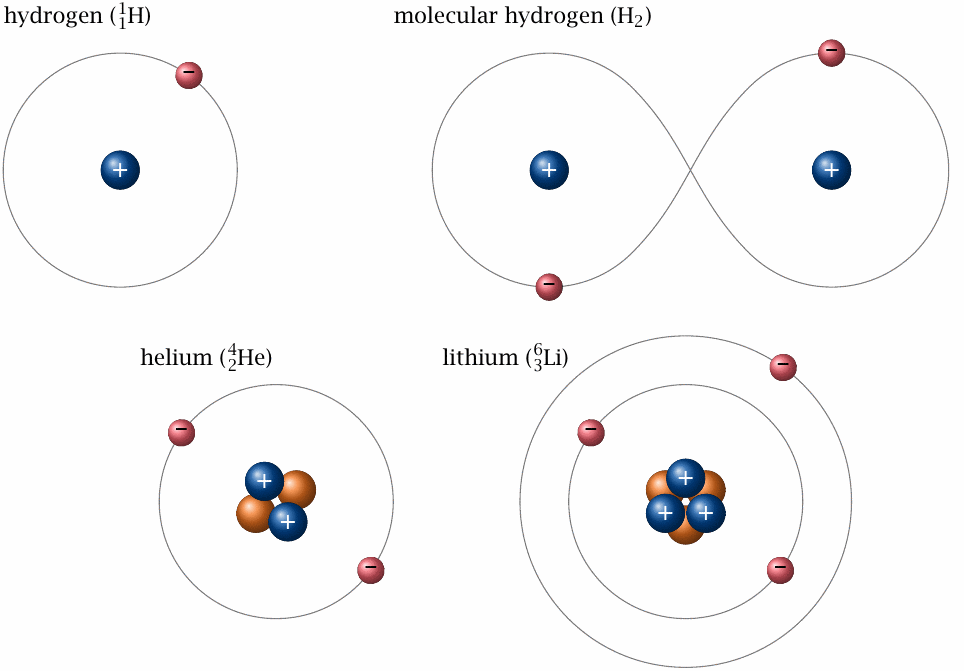
Protons and neutrons are similar in mass but differ in electric (coulombic) charge. Neutrons are uncharged, whereas each proton carries a single positive charge. The magnitude of this charge equals that of the electron; however, the latter’s charge is negative. In the common case that the number of protons in the nucleus equals that of the electrons in the shell, the atom has no net charge. On the other hand, if the atom is short of electrons or has surplus ones, it will have a positive or negative net charge. Atoms (and also molecules) that are in a charged state are called ions.
| 2.2 |
Chemical bonds and molecules |
In everyday chemistry—including biochemistry, that is, the kind of chemical reactions that occur in the human body and other living organisms—only the electron shells of the atoms take an active part; the nuclei are merely passengers. There is a number of rules that govern the behavior of the electrons, and therefore the chemical reactivity of each element. One of these rules states that electrons prefer to form pairs. If all electrons of an atom can form pairs within that atom’s shell, then the element in question typically has low reactivity. An example is helium (shown in Figure 2.1), which occurs in nature as a one-atomic gas. On the other hand, hydrogen and lithium have unpaired electrons in their shells, and they are therefore more reactive. Two hydrogen atoms can mutually satisfy their preference for electron pairing by sharing their electrons within in a joint, dumbbell-shaped orbit (the chemical term is orbital ). The shared electron pair constitutes a chemical bond between the two hydrogen atoms, which thus have become a single hydrogen molecule (H2). Lithium can react analogously with other atoms, although two lithium atoms will not form a stable molecule.
The atoms of some elements have more than one unpaired electron in their shells; for example, oxygen has two, and nitrogen has three. With nitrogen, all of these can be paired in a diatomic nitrogen molecule (N2). To indicate that this molecule contains three shared electron pairs or bonds, N2 may be written as N≡N, while H2 with its single bond is written as H–H.
In contrast to nitrogen, molecular oxygen (O2) does not manage to properly pair all electrons; its electronic structure may be written as •O–O• to indicate that one stable electron pair is formed, while the other two electrons, represented by the dots, remain ‘lonely.’ This difference in internal electron pairing explains the very different reactivities of oxygen and nitrogen, for example vis-a-vis hydrogen: while N2 can be coaxed into reacting with hydrogen only at very high pressure and temperature,20 oxygen requires only a spark to explosively react with hydrogen. The product of this reaction (2H2+O2⟶2H2O) is of course water; its bond structure may be written as H–O–H, which means that in this molecule all the electron pairing needs of oxygen are satisfied. Water is therefore a fairly stable molecule. Oxygen also reacts with carbon (C) to form a stable product, carbon dioxide (CO2, or O=C=O), again with the release of energy; and similarly with many other elements. The wide scope of oxygen’s reactivity is reflected in the familiar observations of combustion and corrosion.
The association between unpaired electrons and chemical reactivity is not limited to the oxygen molecule. Below, we will see that ionizing radiation can break up electron pairs within initially stable atoms and molecules, which thereby become reactive. Before considering the biological significance of this effect, we will first consider the physical basis of radiation and radioactivity.
| 2.3 |
Radioactivity |
While chemical reactivity is determined by the electron shell, radioactivity is a property of the atomic nucleus alone. Most of the atomic nuclei that occur in nature are stable, but some are not; these will at some point in time decay. The stability of a nucleus depends on the ratio of neutrons to protons which it contains, as well as on its overall size, that is, its overall count of protons plus neutrons.
We have already encountered the three isotopes of hydrogen (see Section 2.1). Protium and deuterium are stable, whereas tritium is not, because it has too many neutrons. It therefore decays through the emission of an electron (e−):
| 13H | ⟶ | 23He+e− | (2.1) |
The emission of the negatively charged electron is balanced by changing one neutron to a proton, which creates a positive charge. The neutron excess is thereby remedied; the resulting nucleus, which now belongs to a different element (Helium, He), is therefore stable.21
The electron produced by the decay is catapulted out of the nucleus with considerable energy, which it will dissipate by colliding with atoms and molecules in its path. The energy transferred in these collisions causes additional electrons to be ejected from those atoms and molecules, which will thereby turn into ions. The formation of ions along the path of the emitted particle can be readily detected; hence, this phenomenon is known as ionizing radiation, and nuclides that produce it are called radioactive.
| 2.3.1 |
Radioactive half-life and activity |
The exact time at which an individual nucleus will decay is unpredictable, but the probability that it will decay within a certain time period can be determined, and this is a fixed and characteristic property of the isotope in question. Processes that follow this pattern—decay or conversion of a species at a rate that is directly proportional to its own abundance—can be described by an exponential function:
| \(N_t\) | = | \(N_0 \, e^{-\nicefrac{t}{\tau}}\) | (2.2) |
In this equation, N0 is the number of atoms at time zero (t=0), and Nt is the number remaining after some time interval t. The lifetime τ is the time required to reduce a given number of atoms (N0) of the nuclide in question to the residue N0/e. Alternatively, we can use the nuclide’s radioactive half-life (t1/2), which is the time required to reduce N0 by half.22 In the case of tritium, the half-life is 12.3 years.
Equation 2.2 states that the residual number Nt of a nuclide is an exponential function of time. The first derivative of Nt is the activity (At) of the nuclide:
| \( A_t = \frac{\text{d}N}{\text{d}t} \) | = | \( -\frac{N_0}{\tau} \, e^{-\nicefrac{t}{\tau}} \) | (2.3) |
The activity is measured in units of seconds-1, which in this context23 is referred to as Becquerel (Bq):
| \( 1 \text{Bq} \) | = | \( 1 \text{sec}^{-1} \) |
The derived unit milli-Becquerel (mBq) denotes one thousandth of a Becquerel.
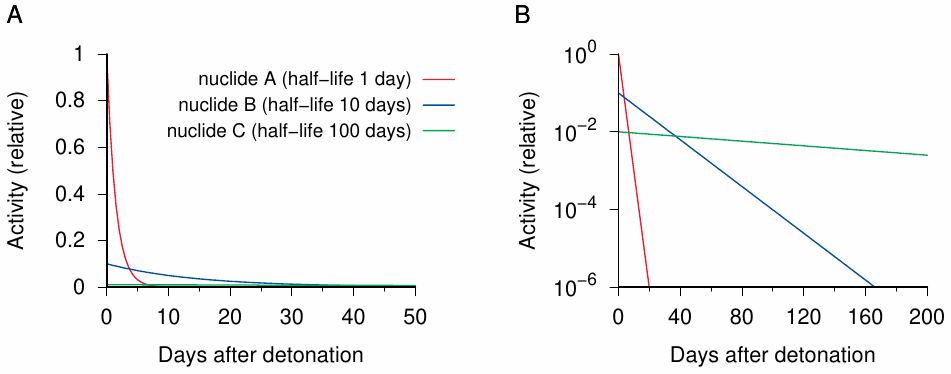
The relationship stated in Equation 2.3 is illustrated in Figure 2.2 for three hypothetical nuclides, which at t=0 are present at the same amounts (N0). Because the lifetime occurs in the denominator of the pre-exponential term, the nuclide with the lowest lifetime—or the shortest half-life; in our example, one day—shows the highest activity per quantity of nuclide, or specific activity. However, after 20 days—that is, after 20 successive half-lives—its activity has dropped to about one millionth of the initial value. On the other hand, the nuclide with the longest half-life (100 days) is still present at appreciable levels even after 200 days.
The half-lives of nuclides occurring in nature or being formed in artificial nuclear reactions vary to a much greater extent than those in our example—namely, from fractions of a second to billions of years. Accordingly, they have vastly different specific activities. Some of the nuclides that are formed by nuclear fission have very short half-lives, and thus cause a ‘flash in the pan’ with very high activity for a very short time, sometimes lasting no longer than the blast itself. Others can be detected for many years afterwards, but because of their relatively low specific activity don’t contribute significantly to the acute radiation dosage.
| 2.3.2 |
Types of radioactive decay |
The form of decay observed with tritium—conversion of a neutron to a proton, with the ejection of an electron from the nucleus—is very common, and it is particularly important with the fission products of uranium and plutonium (see later). It is referred to as β-decay, and more specifically as β−-decay, since the ejected electron is negatively charged.
Some nuclides that undergo β-decay may concomitantly also emit a neutron. While this is comparatively rare, it does occur among the fragment nuclei that result from nuclear fission, and these delayed neutrons form part of the neutron radiation released by nuclear bombs.
In many cases, a nucleus undergoing β-decay does not get rid of all available energy in the process. In these cases, the remainder is emitted, usually a short time later, as a γ-particle, which is a photon—a particle of the same nature as light, but with much higher energy (and correspondingly shorter wavelength). γ-Particles, or γ-rays, can also be produced by nuclei that need to offload surplus energy originating from other processes, including α-decay, nuclear fission, or the non-elastic collision with neutrons (see below).
While the nuclei of tritium and of most nuclear fission products contain excess neutrons and thus undergo β−-decay, the opposite case also occurs. Unstable isotopes that have too few neutrons may achieve stability by ‘reverse’ β-decay, or electron capture. Here, the nucleus picks up an electron from the atomic shell, and one of the protons is thereby converted to a neutron. The nucleus may again release excess energy through γ-radiation. An example is the iodine isotope 125I, which decays to an isotope of tellurium (Te):24
| 53125I+e− | ⟶ | 52125Te | (2.4) |
In α-decay, the emitted particle is larger and heavier than in β-decay—it contains 2 protons and 2 neutrons, and therefore is identical with the nucleus of the stable helium isotope 4He. α-Decay is particularly important with very heavy elements25 such as radium, thorium, uranium, and the artificially produced elements that exceed the atomic number—that is, the proton count—of uranium. These ‘transuranes’ include in particular plutonium, which is produced in nuclear reactors from the uranium isotope 238U through neutron capture and two subsequent β-decays (see below). α-Decay may also be accompanied by the release of γ-radiation.
| 2.3.3 |
Decay chains |
The products of radioactive decay may themselves be unstable and decay in their turn, and successive decays may form a chain that continues for multiple generations. An important natural decay chain begins with 92238U and ends with lead (82206Pb), which is stable. The total number of nucleons declines by 32, which corresponds to 8 α-particles overall. 8 α-Decays would reduce the number of protons by 16, but the actual difference is only 10, which means that 6 neutrons must be converted to protons through β-decay. Accordingly, the total number of α- and β-decays is 14.
The half-life of 238U, at 4.47 billion years, is much longer than those of all intermediate species. This has the interesting consequence that the activities, that is, the number of decays per unit of time, of all chain members in a natural, undisturbed uranium ore sample will be virtually equal. To see why, assume that you start with a sample of pure 238U. As the uranium undergoes α-decay with very low, virtually constant activity, its daughter nuclide (234Th, an isotope of thorium) will accumulate. 234Th has a half-life of only 24 days and will therefore decay rapidly; it can accumulate only until the rate of its own decay—its activity—reaches the rate of its formation, which is of course identical with the activity of 238U. The same principle applies to all subsequent decay intermediates, including the uranium isotope 234U, which is formed two β-decays downstream of 234Th. Therefore, in natural uranium, the activities of 238U and 234U should be equal, even though 234U is much less abundant. We will make use of this relationship when considering studies on the fallout of the Hiroshima bombing (see Section 3.1).
| 2.4 |
Interaction of ionizing radiation with matter |
As briefly stated above, all types of particles released by radioactive decay will cause ionization: as they collide with atoms and molecules along their path, they will transfer some of their initially ample energy to the electrons of those targets, and the electrons will thereby be ejected from their atomic shells, turning the atoms and molecules into ions. Since these ions are readily observed in ionization chambers (see below), all of these disparate particles came to be known as ‘ionizing radiation’. However, they cause other effects beyond ionization, and some of these affect living organisms.
| 2.4.1 |
Radical formation |
Ejection of electrons can happen not only with individual atoms but also with molecules, which may thereby be broken up. A straightforward example is the cleavage of water molecules, which may be written as
| H–O–H | ⟶ | H++e–+•O–H | (2.5) |
What happened here? One electron (e−) that was part of an O–H bond has been ejected. The hydrogen atom has been ionized (H+), and the second bond electron is retained by the residue of the molecule (•O–H, or •OH), whose dot represents this now unpaired electron. An atom or molecule with an unpaired electron is referred to as a radical.
Due to their unpaired electrons, radicals tend to be highly reactive, and none is more so than the hydroxyl radical (•OH). Since water is abundant in living organisms, •OH is the predominant product of irradiation and the most important mediator of its deleterious effects (see later).26
| 2.4.2 |
Interactions of γ-rays with matter |
For the most part, γ-rays cause ionization and radical formation as described above. Most commonly, the interaction with electrons in target atoms will take the form of Compton scattering—the γ-photon collides with an atom or molecule and ejects one of its electrons. In the process, it also transfers some of its kinetic energy to the electron, which causes the γ-photon itself to change direction. This can repeat a number of times until the energy of the γ-photon is depleted.
Since γ-rays dissipate their energy through successive collisions with electrons, it follows that sufficiently thick layers of matter, which contain a large enough number of electrons, can act as a shield against γ-radiation. Since atoms contain equal numbers of electrons and protons, heavy elements make particularly good shields; lead is very commonly used for this purpose.27
| 2.4.3 |
Interaction of α- and β-particles with matter |
Due to their slower speed and their electric charge, α- and β-particles interact with electrons more effectively than do γ-rays. Thus, after entering a target, both particle types produce many secondary ions in rapid succession, at a high local density, and in so doing quickly exhaust their energy. They therefore do not penetrate matter very deeply (see Section 2.7.1).
| 2.4.4 |
Neutron interactions with matter |
Unlike the other particles considered here, neutrons don’t interact with electrons directly, but only with atomic nuclei. The collision of a neutron with a nucleus may have three different outcomes:
- the neutron may bounce off, such that the overall amount of kinetic energy is preserved, but some part of it is transferred to the nucleus. This is known as elastic neutron scattering.
- it may be ‘swallowed up’ by the nucleus. This is known as neutron capture;
- it may be captured briefly but immediately ejected again. This is referred to as non-elastic neutron scattering.
In both elastic and non-elastic scattering, the neutrons will not only lose part of their energy but also change direction.
When neutrons of sufficient energy are scattered elastically by hydrogen nuclei, the latter will be yanked loose from the molecules that they are part of and sent flying; these so-called ‘recoil protons’ then cause the actual ionization and radical formation. This effect mediates most of the biological effects of neutron radiation and also is important for its detection.
Virtually any nuclide can capture a neutron, but the probability varies both with the composition of the target nucleus and the kinetic energy of the neutron. With most nuclides, neutrons of very low energy are captured the most readily. These are called thermal neutrons, since their kinetic energy is in equilibrium with that of the surrounding atoms, whose kinetic energy reflects the temperature of the system. Figure 2.3 illustrates how the probability of capture varies with the energy of the neutron on the loose with two different nuclides, cobalt-59 and uranium-235. These two neutron capture reactions can be written as follows:
| 2759Co+n | ⟶ | 2760Co | (2.6) |
| 92235U+n | ⟶ | 92236U | (2.7) |
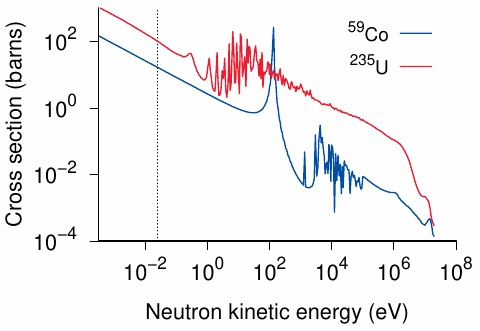
The products of neutron capture are often unstable, and this is the case with both of the above examples. 60Co undergoes radioactive β- and γ-decay with a half-life of 5.27 years. The γ-particles emitted by 60Co are quite high in energy; they can be used e.g. for the irradiation treatment of cancer or for sterilizing medical equipment. With 236U, most nuclei immediately undergo fission (see below); however, a minor fraction of nuclei don’t fission but instead ‘simmer down’ and undergo radioactive decay with a rather long half-life (23.4 million years).
In both the capture and the non-elastic scattering of neutrons, the atomic nuclei are transiently promoted to more energy-rich states; they release this surplus energy in the form of γ-radiation. These secondary γ-rays contribute to the biological effects of neutron radiation.
| 2.5 |
Nuclear fission |
As an alternative to α- or β-decay, some unstable nuclides may undergo nuclear fission. In this process, the nucleus breaks up into two large fragments of somewhat variable size and composition, plus two or three individual neutrons. Most of the nuclear energy released by the fission is converted to kinetic energy, causing the two fission fragments and the neutrons to dash off like scalded cats; some more energy is released in the form of γ-radiation.
Some nuclides may fission spontaneously, while others fission only upon neutron capture. Among the latter, some are fissioned only by neutrons of high energy, whereas others are readily fissioned by any neutrons at all, regardless of their kinetic energy. This leads to the following distinction:
- a fissionable nuclide releases neutrons which are too low in energy to fission other nuclei of the same nuclide.
- a fissile nuclide releases neutrons which can fission other nuclei of the same nuclide; thus, with these nuclides, fission can potentially occur as a chain reaction.
Among the isotopes of uranium, 238U is fissionable, whereas 235U is fissile. 235U is indeed the only fissile nuclide with useful natural abundance. However, additional ones can be produced artificially from certain precursor nuclides; these are called fertile. The most important fertile nuclides are 238U and 232Th, which upon neutron capture undergo two sequential β-decays to turn into the fissile nuclides 239Pu and 233U, respectively.28 In so-called ‘breeder’ reactors, fissile and fertile nuclides are mixed on purpose, and a fraction of the neutrons produced by the ongoing chain reaction is diverted to ‘breed’ more fissile nuclides for use as reactor fuel or bomb material.
While 232Th is more abundant than 238U, there are some technical obstacles to the use of its fissile derivative 233U as bomb material. This leaves 235U and 239Pu as candidates for such use; the Hiroshima bomb (‘Little Boy’) is said to have contained 235U, whereas the Nagasaki bomb (‘Fat Man’) purportedly contained 239Pu.
| 2.5.1 |
Products of nuclear fission |
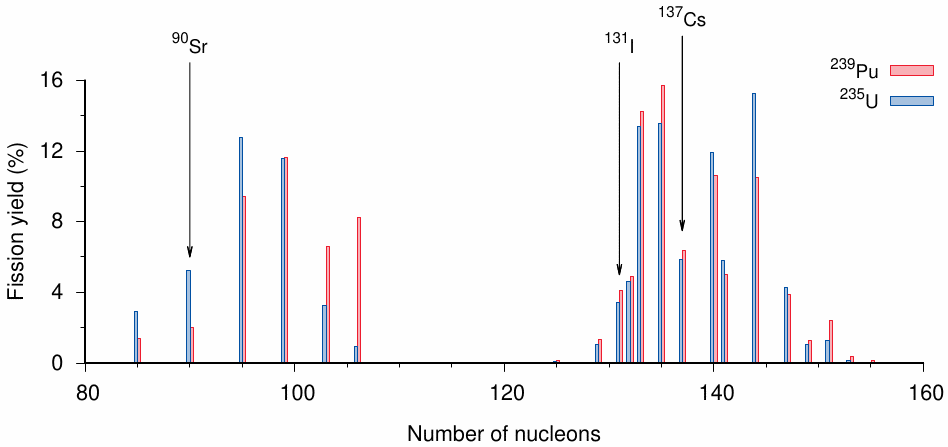
Each fissile nuclide gives rise to a distribution of fission products rather than two distinct species. The shape of the distribution varies somewhat between nuclides and also with the energy of the neutrons that bring about the fission; in particular, it differs between nuclear reactors and bombs, which use low and high energy neutrons, respectively. Figure 2.4 shows the distributions produced by 235U and 239Pu when fissioned with fast neutrons, that is, under conditions similar to those that would prevail in a fission bomb. The fission products fall into two clusters centered near 140 and 95 nucleons, respectively. The two nuclides produce a similar amount of 137Cs, which was already introduced in Chapter 1 as a marker of fallout in environmental samples. In both cases, 137Cs is produced in approximately 6% of all fission events; thus, from the abundance of 137Cs in the fallout, it is possible to estimate the total amount of bomb fuel that must have fissioned.
131I (iodine) and 90Sr (strontium) are fission products that may accumulate in specific organs and potentially cause disease. 90Sr chemically resembles calcium and accumulates in bone mineral; its proximity to the bone marrow may contribute to the causation of leukemia. Its half-life is 28.8 years, which means that it remains detectable in the bone for significant lengths of time. In contrast, the half-life of 131I is only about a week. This is nevertheless long enough for it to be dispersed with the fallout and to accumulate in thyroid gland tissue. Release and dispersal of 131I in the Chernobyl disaster caused numerous cases of thyroid cancers in the adjacent areas of Ukraine and Belarus [45].
Another point to note is that fission products such as the three discussed above will typically not be formed directly. Instead, the immediate fission products tend to be very short-lived and decay into longer-lived ones through one or more β-decays; this is illustrated in Figure 2.5. The γ-rays emitted as part of these secondary decays contribute significantly to the immediate radiation of the bomb. Some of these decay events will also release neutrons; while such ‘slow neutrons’ make only a minor contribution to the bomb radiation, they are crucial for controlling chain reactions inside nuclear reactors.

| 2.5.2 |
Fission bombs |
The detonation of a fission bomb occurs through a chain reaction, which starts when the first 235U or 239Pu atom captures a neutron—supplied by a small neutron source built into the bomb—and undergoes fission. As stated above, this produces two fragment nuclei and 2 or 3 neutrons. Each of the neutrons can potentially be captured by another fissile nucleus and cause it to fission in turn. The likelihood of such secondary fission events depends on the number of fissile nuclei within reach of each liberated neutron. Once this likelihood becomes so high that, on average, each fissioning nucleus will give rise to more than one fission event in the next generation, the chain reaction will be rapidly amplified and cause the detonation. To make this happen, we need to pack enough fissile nuclei next to each other—the amount needed will vary with the identity and the purity of the fissile isotope in question and is referred to as its critical mass.
From the foregoing, we can understand in outline what the consequences of a nuclear detonation will be. The copious kinetic energy of the fission products and neutrons is converted to heat. The heat produces a flash of light, and it also drives expansion of the surrounding air, which gives rise to a pressure shock wave. Much of the γ-rays and some of the neutrons will escape from the detonating bomb core and cause an intense pulse of ionizing radiation. In contrast, the β-particles released by short-lived fission intermediates have only short free path lengths and remain confined within the core. In summary, the immediate long-range effects of a detonating fission bomb comprise intense radiant heat, a shock wave, and ionizing γ- and neutron radiation.
| 2.5.3 |
Fission yield |
We had noticed in Section 1.2 that with the alleged uranium bomb detonated above Hiroshima only about 1 kg 235U of 50 kg had undergone fission, whereas the remainder is said to have been scattered about. Why did this happen?
The chain reaction will only be sustained as long as the critical mass stays together. As soon as the chain reaction begins, it will release heat, which will tend to blow the critical mass apart. A key problem in the construction of fission bombs is to keep the critical mass together long enough for the chain reaction to reach enough of the fissile material. The fraction of the fissile material actually fissioned before the critical mass breaks up is referred to as the fission yield.
| 2.6 |
Ionizing radiation unrelated to radioactivity or nuclear fission |
The particles released by radioactive decay are ionizing primarily due to their high energies; the source of that energy—in this case, the atomic nuclei undergoing decay—is not important. Other, artificial means for endowing particles with similarly high energies exist, and the energy-rich particles thus generated will be every bit as ionizing as those arising from radioactivity.
There is no need for a comprehensive survey of such techniques for our purposes, but some examples are relevant and useful. The process always begins by accelerating a charged particle in a vacuum using high voltage. The easiest such process involves the acceleration of electrons, which then strike a metal target. Within that target, they will collide with other electrons, to which they will transfer some of their energy. The transferred energy is then released in the form of X-rays, which are electromagnetic radiation of high energy. The particle energy of this radiation depends on the strength of the electric field used for electron acceleration, and it can match or even exceed that of γ-rays. Such high-energy X-rays can be used interchangeably with γ-rays in technical or medical applications. Similarly, the accelerated electrons themselves can be used to mimic β-radiation.
The artificial generation of neutrons in the laboratory can be accomplished by stripping some atomic nucleus of electrons and then using an electric field to accelerate it and slam it into another nucleus. Most commonly, this is done with two isotopes of hydrogen (deuterium and tritium); the collision of the two nuclei will produce helium and a free neutron. In the early days, including those following the alleged atomic bombings, the production of neutrons in quantity required cyclotrons, but in the meantime smaller, simpler devices have been invented. Such artificial neutron sources can be used to mimic, and thus to study, the effects of neutron radiation from atomic bombs.
The process of charged particle acceleration by an electric field also makes plain the meaning of the physical unit electron volt (eV)—it is equivalent to the energy which an electron, or another particle with a single charge, will acquire while traveling through a vacuum from one electrode to another when a potential of 1 V exists between the two. The energies of particles released by radioactive decay are typically stated in kilo-eV (keV) and mega-eV (MeV; one million eV). For example, the decay of 60Co produces β-radiation with 317 keV as well as γ-radiation with 1.17 MeV and 1.33 MeV. We can mimic those β-particles by sending electrons down a field with 317 kV, and the γ-radiation by accelerating electrons using 1.17 or 1.33 MV and then converting them to X-rays by slamming them into a metal target.29
| 2.7 |
Attenuation of ionizing radiation by matter |
When a particle of ionizing radiation impinges on some target matter, it will begin to ionize the atoms and molecules within; and since each ionization event requires some energy, the ionizing particle itself will eventually run out of energy and come to rest or vanish. To what depth the particle can penetrate before this occurs obviously depends on its initial energy; in addition, however, it also depends on its nature, which determines at what range it can interact with individual electrons or nuclei in the target matter.
| 2.7.1 |
Distinctions between particle types |
The interaction with the longest range is the Coulomb force; accordingly, α- and β-particles, which are electrically charged, interact the most readily and produce the greatest number of ions along a certain path length. This also means that they shed their energy very quickly and thus penetrate the target matter only to a very shallow depth. Among the two, the α-particles are heavier and slower; they thus spend more time in the vicinity of a given single electron and stand a greater chance of exerting enough pull to pry it loose from its host atom. Therefore, α-particles exhibit the highest density of ionization, which implies the shallowest depth of penetration; in fact, they cannot even penetrate intact human skin deep enough to reach its basal layer of vital, regenerating cells. Isotopes that emit α-radiation thus can harm humans only when ingested or inhaled.
The lighter β-particles move faster and do not ionize quite as many atoms or molecules along a given stretch of path within the target, which results in somewhat deeper penetration. Even they, however, will penetrate human skin to a depth of only a few millimeters; thus, while β-emitting radionuclides may burn the skin from without, they may cause damage to interior organs only after they have been taken up. This is illustrated by the aforementioned fission products 131I and 90Sr, which will cause disease only after accumulation in the thyroid gland or bone matrix, respectively.30
In contrast to α- and β-particles, γ-photons have no charge, and they thus will interact with electrons only when they hit them straight on. Thus, on average, a γ-photon will travel a much longer distance between two consecutive ionization events; it will shed its energy more slowly and penetrate the target to a much greater depth, or even traverse it. The depth of penetration will be inversely proportional to the number of electrons per volume segment of target matter; thus, matter that consists of comparably light atoms, for example water or soft tissues, will be penetrated most readily, whereas matter that contains heavier atoms such steel or bone mineral stop γ-rays more readily.31
Neutrons are uncharged as well; unlike γ-rays, they interact primarily with the nuclei of the target matter, and moreover they lose energy more readily by colliding with lighter nuclei than with heavier ones. Like γ-rays, however, they can penetrate the walls of buildings and human tissues to considerable depths. Both neutrons and γ-rays thus contribute to the total radiation dose due to a nuclear detonation.
| 2.7.2 |
Linear energy transfer |
We just saw that ionizing particles differ in their depth of penetration into a target, and we explained this in terms of faster or slower depletion of a particle’s energy. This can be expressed quantitatively as the amount of energy transferred from the impinging particle to the matter in the target as it traverses a certain specified distance. This quantity, the particle’s linear energy transfer, correlates inversely to its depth of penetration.
| 2.7.3 |
Quantitative treatment of attenuation |
Let us first consider a parallel beam of radiation that strikes a block of matter, whose surface is perpendicular to the beam. As a first approximation, we can consider the block of matter as composed of many stacked layers of uniform thickness, and then postulate that each layer attenuates the impinging radiation by a constant fraction or percentage. This results in an exponential relationship: just as we can determine a lifetime for the effect of time on radiation intensity, we can determine a relaxation length for the shielding effect of matter:
| \( R_d \) | = | \( R_0 \, e^{\,\nicefrac{d}{\lambda}} \) | (2.8) |
In this equation, R0 is the unattenuated radiation intensity at the surface, d is a certain depth of penetration, Rd is the radiation intensity observed at that depth, and the relaxation length λ is the layer thickness of the given material that will reduce R by a factor of 1/e. In analogy to the half-life that describes the effect of time, we can also define a half-thickness that will reduce radiation intensity by a factor of 1/2. Furthermore, one may find values tabulated for layer thicknesses that attenuate radiation by 90%; this latter value will be approximately 3 times the half-thickness.32
From the preceding sections, it will be clear that the actual values of relaxation lengths and half-thicknesses will vary greatly both with the type of radiation and the shielding material. The principle applies not only to solids or liquids, but also to gases, including the atmosphere; the difference is simply that the shielding half-widths or relaxation lengths in the atmosphere will be far larger than for example in water, soil, or concrete. While the exponential approximation thus is quite versatile in practice, there are some effects that limit its accuracy:
- Particle energies are usually inhomogeneous, and particles with higher energies will penetrate more deeply.33
- Even if all particles strike the surface of the block of matter in question from the same direction, they may be scattered rather than fully stopped; they will thus change both their energy and their direction.
- Some primary particles, when stopped, will produce secondary radiation: stopped β-particles or fast electrons will produce X-rays, and stopped neutrons will produce γ-rays. These secondary rays will typically be more penetrating than the primary particles that produced them.
These effects need to be taken into account in order to accurately determine the dosages received for example by persons located inside a house during a nuclear detonation, as discussed by Auxier [36]. Nevertheless, the exponential approximation is useful at least for orientation.
| 2.7.4 |
Concomitant attenuation and radial divergence |
Equation 2.8 describes the attenuation of a parallel beam of radiation. However, in the detonation of a bomb, the radiation propagates in all directions, diverging radially from the center. Let us assume a nuclear bomb goes off in outer space, where there is no matter that could attenuate its radiation. Then, due to the radial divergence, the radiation intensity Rd will still decrease with increasing distance d:
| \( R_d \) | = | \( \frac{1}{d^2}\,R_0 \) | (2.9) |
If we assume that d is given in meters, then R0 is the radiation intensity at a distance of 1 m from the center of the detonation, since here 1/d2 = 1. This assumption treats the exploding bomb as a point source, which is of course not realistic; however, in practice we are only interested in the radiation intensity at much larger distances from the bomb, where the point source assumption is good enough.
When a bomb goes off in the atmosphere, both attenuation and divergence must be considered. We can account for their combined effects with the following formula:
| \( R_d \) | = | \( \frac{1}{d^2}\;R_0\;e^{\nicefrac{-d}{\lambda}} \) | (2.10) |
R0 has the same meaning as in the preceding formula. Equation 2.10 applies to both neutron and γ-radiation released by a bomb, but of course each kind of radiation has its own characteristic λ value. Furthermore, the equation can be used to estimate both the number of ionizing particles per unit area, referred to as the fluence of the radiation, and the dose received by some body of matter struck by these particles (see Section 2.9). We can rearrange Equation 2.10 as follows:
| \( R_d \, d^2 \) | = | \( R_0\,e^{\nicefrac{-d}{\lambda}} \) | (2.11) |
The product Rd d2 is a simple exponential function of d, which in a semilogarithmic plot will yield a straight line. From the slope of this line, we can obtain λ. This approach will be used in Section 6.1.1.
| 2.8 |
Measurement of ionizing radiation |
In order to detect and quantify ionizing radiation, we must observe some of its interactions with matter; and to do so sensitively, we must find ways to amplify the initial signal generated in this interaction. Several different physical principles are exploited for these measurements.
| 2.8.1 |
Ionization |
This effect is observed in an ionization chamber, an enclosure that is filled with some noble gas and also hosts two electrodes, between which a high voltage is applied. When an ionizing particle traverses this chamber, it will collide with gas atoms and knock electrons out of their shells. In the strong electric field, the ions and the electrons will become separated and be attracted toward the two opposite electrodes, where they will cause an electric signal. The magnitude of this signal will be proportional to the number of ions that were generated; and this number will vary depending on the type and energy of the ionizing particle as outlined above.
In what form exactly the signal is received depends on the experimental setup. If the voltage between the electrodes is applied only initially but not renewed, then each detected burst of ions and electrons will decrease that initial voltage. This means that the measurement will be cumulative—we will know how many ions were generated, but not by how many ionizing particles. If the voltage is kept constant, then the signal is the current required to restore the voltage to its preset level after each ionization event; and since this restoration will occur quickly, it will be possible to count the number of ionizing particles over a certain time interval.
Even though it may be counterintuitive, the signal can be amplified by reducing the gas pressure inside the chamber. A low pressure will reduce the number of collisions between the ionizing particle and the gas atoms, and therefore the number of ions and electrons released; however, while traveling toward their respective target electrodes, these secondary ions will gather more speed before colliding with other gas atoms, and due to this greater speed they will be able to ionize those gas atoms in turn. The overall result will be a cascading proliferation of charged particles and therefore amplification of the electrical signal. There are two ways to exploit this mode of amplification:
- The amplification may be limited in extent, such that the final signal is still constrained by the number of ions and electrons generated directly by the ionizing particle. Then, the signal will retain information about the nature and energy of the ionizing particle.
- The amplification may be saturating—each event is amplified to the same, maximal extent, regardless of the strength of the original ionization. This will maximize sensitivity, but on the other hand the ability to discriminate between different particle types is lost. This latter principle is applied in the widely used Geiger counters.
Both modes of detection have their uses. Generally speaking, counting devices optimized for sensitivity tend to be simpler and are more suitable for field use. Instruments that can discriminate different particle types are more complex and mostly used in the lab. The key advantage is that particle energies can be used to discriminate and identify different radionuclides in complex mixtures such as soil, which may contain both natural background and nuclear fallout; Figure 3.3 shows an example.
| 2.8.2 |
Scintillation |
Like ionization, this physical effect begins with a collision of an ionizing particle with an electron of some other atom or molecule. However, in scintillation, the electron is not knocked free but only transiently promoted to a higher state of energy within its host particle. When it falls back to its initial level, the surplus energy which it received in the collision is released as light (a single photon). The light can be focused onto a photomultiplier and quantified; the intensity of the flash of light will be proportional to the number of scintillating atoms or molecules and thus to the energy of the ionizing particle. γ-Rays induce intense scintillation in materials such as crystalline sodium iodide, and this is exploited for their detection.
| 2.8.3 |
Thermoluminescence |
Some materials, particularly ceramic ones, may show a peculiar response to ionizing radiation: the dislocated electrons may migrate through the material for some distance and become trapped in a metastable state, that is, a state that is high in energy, yet unlike most other high-energy states does not spontaneously fall back to a lower energy level. It can, however, be induced to give back its energy in the form of light by heating the material. This heat-induced light signal is called thermoluminescence.34
The metastable state can persist for potentially very long periods of time, which means that it gives the material a ‘memory’ for the ionizing radiation it was exposed to in the past. Ceramic material is fairly dense and thus will not be significantly penetrated by α- or β-radiation. Neutrons and γ-rays may penetrate it, but of these only γ-rays interact with electrons effectively; thus, in practice, all the observed thermoluminescence activity can be attributed to γ-rays.
An interesting application of thermoluminescence concerns the dating of ceramics recovered in archaeological excavations [47]. Firing a new piece of pottery will purge the clay of any previously accumulated luminescence energy and thus ‘reset the clock’, and its repeated heating on a fire while in use will do the same. Once it becomes emplaced underground, however, its pent-up thermoluminescence will increase at a steady rate due to the decay of natural radioactive isotopes such as 40K within the material itself and in the soil around it. When the piece is heated again after its recovery, the amount of light released will be proportional to the number of γ-particles that struck it, and therefore to the time elapsed, since it became buried.
When applied to tiles and bricks of recent manufacture, the luminescence induced by natural radiation should of course only amount to negligible background, and in a sample from Hiroshima or Nagasaki, the lion’s share of the signal should come from the intense flash of γ-rays that it was exposed to when the bomb went off. We will consider experimental studies of this kind in Chapter 5.
| 2.8.4 |
Mass spectrometry |
This method does not measure radiation as such, but it can nevertheless be used to determine the presence and abundance of radionuclides in a sample. As the name suggests, mass spectrometry simply distinguishes atoms—or, in other applications, molecules—according to their mass; it can therefore be used with both stable and unstable nuclides. The method requires that all atoms be converted into single ions, then accelerated in an electric field, and finally captured in a detector. The crucial step for identification is the acceleration: it must overcome inertia, which is proportional to mass; therefore, between two atoms of equal charge but different mass, the lighter one will reach the detector before the heavier one.35
Mass spectrometry is very powerful and versatile; nevertheless, it has not fully replaced radiation counting. To understand the respective advantage of either method, consider that radioactive isotopes decay on vastly different time scales (Section 2.3.1). Among the fission products of 235U, a short-lived nuclide is 131I, which has a half-life of 8 days, whereas a long-lived one is 129I, which has a half-life of 16 million years. (Both are isotopes of iodine.)
Assume we have a sample that contains 1 ppm (one millionth) of 131I, while the remainder is 129I. Mass spectrometry will simply count the atoms as they are at any given moment, and will give us the true abundance right away—but the very small fraction of 131I in our sample might get lost in the noise. On the other hand, if we use radiation counting, the far shorter half-life of 131I means that many more of its atoms will decay during the time interval of the measurement—indeed, even at these odds, its signal will be about 700 times higher than that of 129I; and with a small sample, we might entirely miss the 129I. This effect is no mere curiosity; for example, in order to measure uranium isotopes in soil samples, radiation counting would be preferred with the relatively short-lived 234U, whereas mass spectrometry would be more suitable for the longer lived isotopes 235U or 238U.
| 2.9 |
Radiation dose |
We have seen that ionizing particles can interact in various ways with matter. While these distinctions are often important, it is also useful to have a global measure of the overall dose of radiation received by a target, and in particular by living organisms. Since each of the interactions between radiation and matter involves some transfer of energy, we can use the sum of all the energy transferred to measure the total dose. The unit of measure is the Gray, or Gy for short; 1 Gy is defined as 1 J/1 kg.
To understand how much, or rather how little, energy 1 Gy actually amounts to, consider this: 1 J is approximately equal to 0.25 cal, and thus will heat one gram of water by 0.25∘C. Accordingly, a kilogram of water that receives a radiation dosage of 1 Gy will thereby be heated by approximately 0.00025∘C. With γ-radiation, the lethal dose in humans is on the order of 8 Gy; therefore, a lethal dosage of γ-radiation will heat up the body by an entirely imperceptible 0.002∘C. Thus, the total energy associated with a lethal radiation dose is minuscule; it is the very high energy associated with each of the individual ionizing particles that makes them so fearfully effective.
| 2.9.1 |
Dose and Kerma |
We just saw that the dose is defined in terms of energy transferred from ionizing particles to a unit of target mass. In this context, one can make a subtle distinction: the energy thus transferred may remain in that target mass unit, or it may escape it in the form of secondary radiation (see Section 2.7.3). The escaping fraction of the energy is included in the kerma, which is an acronym for ‘kinetic energy released per unit mass’, but it is excluded from the dose.
How important is this distinction with human bodies? We have relatively large bodies; therefore, much of the energy that will escape one kg-sized portion of our body will end up in the next, and vice versa. Therefore, fruit flies and silkworms probably have more reason to worry about the difference than we do; for the purpose of this book, we can treat the two as approximately equivalent.
| 2.9.2 |
Biological effectiveness of different particle types |
Qualitatively, all types of radiation induce the same kinds of genetic damage in cells (see below); however, if we use identical doses of each as measured in Gy, then the extent of the damage will vary considerably. To account for this, biological weighting factors have been distilled empirically for each type of radiation from experimental observations (Table 2.1). These weighting factors go by various names; we will here adopt relative biological effectiveness (RBE). In order to estimate the biological effect of a given physical dose of radiation, one multiplies the physical dose in Gy with the appropriate RBE:
| biological dose (Sv) | = | RBE × physical dose (Gy) | (2.12) |
| Radiation type | RBE |
| α-particles | 20 |
| β-particles | 1 |
| photons (γ-rays and X-rays) | 1 |
| neutrons | 5 |
Since the RBE factors are dimensionless, the unit of the biological dose—the Sievert, or Sv for short—is also equal to 1 J/1 kg, as is the Gray. Which unit to use depends on the context. It probably goes without saying that the numbers listed in Table 2.1 are approximations. With neutrons, there is considerable debate about the most appropriate value. In Figure 8.1, we will use the dose-adjusted RBE described by Sasaki et al. [48], but the neutron RBE value listed here, 5, is a reasonable approximation in the relatively high dose range that matters most in this book.
| 2.10 |
Forms of radiation released by fission bombs |
While fission bombs may of course be detonated anywhere, we will confine the discussion to air bursts at considerable altitude, as allegedly occurred in Hiroshima and Nagasaki.
| 2.10.1 |
Immediate radiation: γ-rays and neutrons |
While inside the bomb itself there is a veritable stew of particles (see Section 2.5), the β-particles and the fission fragments have low ranges within the bomb and even within air, and they will not contribute to radiation on the ground. In contrast, both γ-rays and neutrons can escape the bomb and strike the ground; it is these two particles that account for the intense yet short-lived burst of immediate radiation from the bomb. Exactly what share of the neutrons will escape the bomb and contribute to radiation on the ground remains uncertain and contentious. For several decades after the event, it was proclaimed that at Hiroshima the biological dose due to neutrons had roughly been on par with that due to γ-irradiation, but later on the neutron dose was revised downward to an almost negligible quantity [49]. This strange story will be examined in Section 11.5.
| 2.10.2 |
Nuclear fallout |
With fission bombs of the size said to have been used in Japan, the fireball of the detonation is expected to reach a maximum diameter of approximately 200 m. Since both bombs were set off at an altitude of at least 500 m, the fireball did not touch the ground.36 Most of the radioactive witches’ brew therefore would not have come down in the targeted cities themselves, but instead have been carried upward in and away by the thermal updraft that was caused by the heat released by the bomb itself. However, some radioactivity did reach the ground as local fallout, carried at least in part by the black rain already mentioned in Section 1.2.
| 2.10.3 |
Induced radioactivity |
Some of the neutrons released by the detonation will strike the ground and, often after first losing most of their energy through a series of collisions, they will be captured by some nuclides on the ground. In many cases, the new nuclides formed by the capture will be radioactive; and since they will tend to have a neutron surplus, they will undergo β−-decay, which is often accompanied by significant γ-radiation. Interest in this induced radiation is twofold:
- at least for a short time after the detonation, some very short-lived nuclides may contribute to the radiation dosage received by people on the ground;
- since radionuclides will be induced in proportion to the intensity of the neutron radiation from the blast, the abundance of the longer-lived isotopes can be used to estimate the neutron dosages that would have been received during the blast.
As noted in Section 2.4.4, the efficiency of neutron capture varies both with neutron energy and with the precursor nuclide in question; some precursors capture only high-energy neutrons, others only or preferentially low-energy neutrons. Comparing within a single sample the abundance of nuclides induced by neutrons of low and high energy, respectively, can give an indication of the neutron energy spectrum of the detonation. Studies which applied this approach to tile or rock samples from Hiroshima have yielded conflicting results (see Section 6.4.2).
| 2.11 |
Biological radiation effects |
| 2.11.1 |
DNA damage and repair |
We have already seen that ionizing radiation converts molecules to radicals (Section 2.4.1). An abundant and particularly reactive radical species is •OH, which is formed from water. While •OH reacts with virtually anything in the cell, including protein molecules and cell membranes, its most significant target is DNA. This is not due to any particular chemical reactivity of DNA, but solely to its special biological function. Other molecules, when damaged, can always be replaced, but DNA cannot—it is passed on from one generation of each cell and each organism to the next, and thus it must be safeguarded from any damage, since even a small chemical change to a stretch of DNA (a gene) can cause a heritable mutation with potentially grave consequences.
Living organisms have been exposed to natural radiation throughout evolution, and accordingly they have developed a fairly elaborate machinery for coping with DNA damage by radiation. This machinery continually scans the DNA for damage. If it is found, the response to it depends on the extent of the damage. If it is deemed limited, then the cell will attempt to repair it. In many cases, this repair will be completely successful and restore the native, intact state of the DNA; the chances for this are good if one of the two DNA strands has remained unaltered and can therefore serve as a template in the repair of the other. On the other hand, if both strands of a DNA molecule are severed, the cell may still succeed in repairing the break and restoring an intact DNA molecule, but the all-important nucleotide sequence may have been altered on both strands. Once this happens, the lesion will have become permanent—a mutation has occurred that will now be passed on to all daughter cells.
An •OH radical can readily break a single DNA strand, and if the local concentration of such radicals is high enough, then two breaks may occur simultaneously on opposite strands, producing the double strand break situation described above. This is the reason why α-particles, which deposit all their energy along a very short distance and therefore produce a high local •OH concentration, have a very high relative biological effectiveness. Thus, overall, •OH radicals are a chief mediator or DNA damage caused by ionizing radiation.37
| 2.11.2 |
Apoptosis |
While DNA repair may seem like an ‘obvious’ coping strategy, a more surprising one is apoptosis, or programmed cell death. Each cell in the human body that contains DNA38 will commit harakiri when the load of DNA damage, and therefore the chance of harmfully mutated progeny, becomes too great. A key effect observed in apoptotic cells is the destruction of the cell nucleus, which contains the DNA; this can be observed by conventional light microscopy, but also at the molecular level as DNA fragmentation.
Intriguingly, cells in different tissues differ significantly with respect to the level of DNA damage beyond which they will abandon repair and initiate apoptosis instead. This tissue-dependent threshold largely accounts for the observed order of organ damage by high doses of radiation. Among major organ systems, the bone marrow is affected first, and with it the regeneration of all types of blood cells; mucous membranes in the intestine are the second most susceptible. And again, since this response to DNA damage is built into the various tissues themselves, it is understandable that DNA-damaging agents other than radiation (such as sulfur mustard, of course) will produce a similar pattern of organ damage.
| 2.11.3 |
Cell proliferation rate and radiosensitivity |
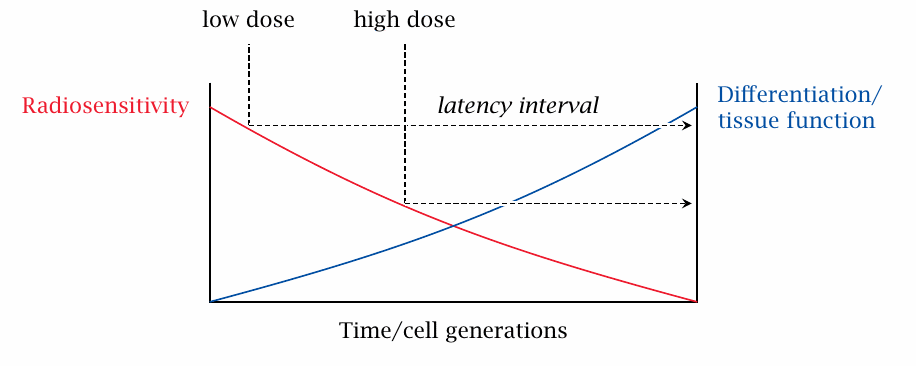
Differences in radiosensitivity exist not only between tissues but also within them. In a tissue that actively regenerates, the cells form a continuum of subpopulations, which ranges from rapidly dividing, undifferentiated cells to those that no longer divide but are fully differentiated (Figure 2.6). The most rapidly dividing cells are also the most sensitive to radiation; the differentiated cells, which have acquired all tissue-specific traits they need to function as that tissue’s ‘worker bees’, have low sensitivity to radiation.
If the tissue is exposed to a relatively low radiation dose, then only the most sensitive, least differentiated cells may be killed off. The partially differentiated cells will go on maturing and sustain the tissue function a while; this corresponds to the clinical observation of a latency period, during which an irradiated patient may appear to be stable or improving. A higher dose will harm some partially differentiated cells also, and therefore shorten this clinical latency period. Moreover, it will more likely kill off every last one of the undifferentiated cells, the stem cells, from which all differentiated ones originate, and thereby cause irreversible, lethal damage to the tissue. These observations are directly relevant to acute radiation sickness.
| 2.11.4 |
Deterministic and stochastic radiation effects |
While each individual event of DNA damage due to ionizing radiation is fundamentally stochastic, some of the overall biological effects are subject to the law of large numbers even in individuals, and they therefore manifest themselves in a predictable, deterministic manner. Any DNA lesion will promote apoptosis regardless of its exact location on the genome. All that is required to pull the trigger is that the number of DNA lesions exceed a certain cell type-specific threshold; and the number of lesions follows the radiation dose in a predictable manner. Furthermore, since apoptosis is the underlying mechanism of acute radiation sickness and of embryonic death or malformations, these, too are governed by deterministic dose-response relationships; both will become manifest in most individuals at doses above 2 Gy (see Sections 8.2 and 12.1). Also in this deterministic category is radiation-induced cataract (see Section 12.3.2).
In contrast, radiation-induced DNA damage has to affect very specific genes in specific ways in order to transform a normal cell to a cancerous or leukemic cell. Only a very small fraction of all damage events will have such specific effects; and therefore, cancer and leukemia are fairly rare even among those exposed to high doses of radiation. Furthermore, most cancers are initiated by cells that have undergone not one but several mutations before becoming manifestly malignant. Irradiation may have contributed some of these mutations, but additional ones were needed to express the malignant phenotype; therefore, cancers and leukemias become manifest with a delay of several years or even decades after the event, during which the cells in question will accumulate additional mutations.39
While cancer and leukemia are stochastic events in individuals regardless of the radiation dose, they should of course have their own law of large numbers in populations. However, the exact dose-response relationship between radiation exposure and cancer remains debated to this day, and not many studies can claim to have surveyed appropriately large populations (see Section 12.1.5).
| 2.11.5 |
Similarity of DNA damage induced by radiation and by sulfur mustard |
We had noted above that DNA double strand breaks are the key mechanism by which ionizing radiation causes mutations and cell death. In this context, we should note that, although the underlying chemistry is different and no •OH radicals are involved, sulfur mustard can also produce DNA double strand breaks [52]. This observation can explain the striking similarities of its biological effects to those of radiation. The reaction of sulfur mustard with DNA and with other molecules in the human body will be considered in more detail in Chapter 7.